分享一篇关于阻抗匹配原理的文章

[小鱼]

罗伯特曾为一位客户解决过一个阻抗匹配的问题。正是这次经历促使他深入研究这个主题，并撰写了这篇关于阻抗匹配基础的指南。

爱因斯坦曾说过：“大多数科学的基本理念本质上是简单的，并且通常可以用一种人人都能理解的语言表达出来。”我不确定这种说法是否仍然适用于21世纪的物理学（试着找到一个能用简单术语解释超弦理论的人）。然而，这也是我写这篇文章的信条。我努力用简单的术语来呈现复杂的概念。本着这种精神，让我们来解决一个棘手的问题。

在过去的十年里，我多次讨论过阻抗匹配的话题。本月，我将再次讨论这个主题。为什么？因为它经常被误解，或被认为是黑魔法。其实不是。阻抗匹配既简单又基础。而且，它不仅仅是射频或超高速设计师的关注点。在接近直流电（DC）的情况下也会出现。你想要一个证明吗？就在一个月前，我们的一位客户在一个特定的开关电源上遇到了效率问题。猜猜是什么问题？是阻抗不匹配问题。我们在适当的位置添加了一个小电感，又赢得了一位满意的客户。

请坐下。在本文中，我将提醒您关于阻抗匹配的基本知识。我将只讨论音频频率范围内的内容，这样你可以轻松地重现和测试我的例子。

基础知识

让我们从最基本的例子开始：直流电。假设你有一个电压为U0的电池，比如12V。不幸的是，完美的电源是不存在的，所以这个电池有一个1Ω的内阻（RIN）。这意味着在无负载时电池电压是U0 = 12V。在1A负载时电压为11V，依此类推。假设你使用这个电池作为电源，并将其端子连接到一个外部电阻R上（见图1）。然后应用欧姆定律是很简单的。电路中的电流为：

[ I = \frac{U_0}{R_{IN} + R} ]

在外部电阻R上消耗的功率很容易计算：

[ P = R \times I^2 = R \times \left( \frac{U_0}{R_{IN} + R} \right)^2 ]

图1是一个带有直流电源的最简单阻抗匹配例子。为了在这个负载中获得最大的耗散功率，负载R的值是多少？

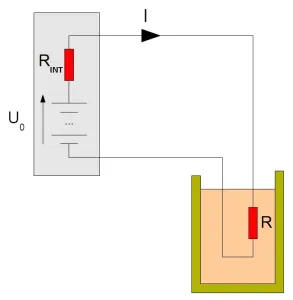
现在想象你不能改变电源的内阻RIN，但希望在电阻R上耗散尽可能多的功率。这意味着你想将尽可能多的能量从电源传递到负载。你的选择是什么？如果你使用高值的R，那么通过它的电流会很小，所以耗散的功率也会很低。相反，如果你使用一个非常低值的电阻（接近短路），那么电路中的电流会非常高，但在电阻上耗散的功率也会非常低。实际上，在后一种情况下，会耗散很多功率，但主要是在电池的内阻上，而不是在外部电阻上。在方程式2中，无论R = 0还是R = 无穷大，P都是零。所以，R必须有一个中间值，以在外部电阻上获得最大的功率耗散，即从电池到负载的最佳功率传递。这就是阻抗匹配，最佳值是R = RIN。你可以自己检查，通过绘制函数R/(RIN + R)^2，或检查其导数在R = RIN时是否为零（即，如果你记得如何计算导数）。

简而言之，从直流电源提取尽可能多的功率的最佳负载是与该电源的内阻相同的电阻值。在我的例子中，12V电池内阻为1Ω，你必须使用1Ω的负载。电路中的电流将是6A（即I = 12V/(1 + 1Ω)）。负载上的耗散功率将是36W（即P = R × I^2 = 1 × 6^2）。任何其他负载值将产生较低的传递功率。

这一基本结果适用于任何需要优化功率传递的情况。这并不意味着你必须总是匹配源和负载的阻抗，但如果你的目标是从源中获得尽可能多的功率，你应该这样做。当然，如果你能减小源的内阻，你可以获得更多的功率，但在这里假设这是不可能的。

从DC到1kHz

如果我们从直流电转到交流电，情况几乎是一样的，只是用阻抗代替电阻。如果你有一个给定阻抗ZS的电源，并将其连接到一个给定阻抗ZL的负载，那么功率传递将在两者阻抗匹配时达到最大。

基本上，这与直流电一样。你知道阻抗Z是电阻R和可能的电抗X（电容性阻抗为负，电感性阻抗为正）之和。我们通常使用复数来简化符号表示，并写成：

[ Z = R + jX ]

不要害怕j变量。只需将其视为以一种单一表达方式管理一对独立值（在这种情况下是R和X）的简便方法。

对于直流电，我们看到当源和负载电阻相等时阻抗匹配。在交流电中，当源和负载阻抗是所谓的复共轭时，阻抗是匹配的。这只是意味着两个电阻应该相等，如在直流电中一样，并且两个电抗应该数值相等但符号相反。换句话说，稍微电容性的源必须与稍微电感性的负载匹配，反之亦然。

现在是例子时间。假设你有一个1kHz的正弦源，幅度为±10V，串联阻抗为1kΩ。如果你想从中提取尽可能多的功率，那么你必须使用一个1kΩ的负载，没有电抗。我使用免费的QUCS电路模拟器为你做了一个小模拟（见图2）。示波器显示了通过两个虚拟表测得的负载电阻上的电压和电流波形。在这里，电压是±5V（因为源和负载电阻都是1kΩ，形成了一个二分之一分压器），电流是±5mA。我添加了一个小方程来计算负载中耗散的RMS功率（在这种情况下为12.4mW）。这是你能从这个源中获得的最大值。

一个不匹配的负载

好吧，让我们保持相同的源（1kHz，10VPP，1kΩ），但将其连接到一个4Ω的负载。会发生什么？模拟结果显示在图3中。负载的阻抗远低于1kΩ，因此源的内阻上的电压降变得非常高，施加在负载上的电压仅为±40mV。电路中的电流是±10mA，但负载中的总RMS功率从12.4mW大幅减少到0.197mW。

这是一个阻抗不匹配问题的好例子。你可以轻松地重现它。打开你的低频发生器，设置为1kHz（或使用你的PC的音频输出），添加一个1kΩ电阻来模拟高输出阻抗，并连接一个4Ω扬声器。我确信你需要靠近扬声器才能听到任何声音。

想象你既不能改变源的1kΩ阻抗，也不能改变负载的4Ω阻抗。你如何改善这种情况（即向负载传递的能量）？通过在它们之间添加一个阻抗匹配网络。这样的网络必须将1kΩ阻抗变成4Ω阻抗。这个过程必须尽可能少地增加额外的损耗，所以不要考虑添加其他电阻。可能吗？是的，确实如此，有两种主要的解决方案。

第一个是简单地使用变压器。想想看，高阻抗意味着电压高电流低，而这正好是低阻抗的相反。因此，在我的例子中，你可以使用一个源侧线圈比负载侧线圈多的变压器。这将降低电压并增加电流，从而降低阻抗。更确切地说，初级和次级匝数比必须是阻抗比的平方根。在这种情况下，是15.8（即√（1000/4）= 15.8）。你可以自己尝试，例如，使用一个小的230到15V的变压器，其匝数比为15.3（即230/15）。这应该显著提高音量。

变压器实际上是一个非常好的阻抗匹配解决方案，因为

它可以在宽频范围内工作。它确实广泛用于音频应用，从电子管放大器到麦克风或高功率音频分配网络。但是，假设变压器对你的应用来说太笨重或昂贵，那么第二种解决方案就有意义了。只使用两个无源部件，既可以是电感器也可以是电容器，我会在一分钟内向你展示如何操作。理论上，这种方法总是可行的，但它有两个缺点。首先，根据不匹配情况，部件值可能不总是现实的，其次，这样的无源匹配网络本质上是窄带的。这意味着它仅在特定频率范围内工作。让我们看看在我的例子中如何使用这种方法。

计算这样的匹配网络最简单的方法是使用在线计算工具。www.leleivre.com有一个很好的工具（见图4）。在这里，我输入了设计数据：1kHz频率，1kΩ源和4Ω负载。然后，工具提出了两种LC网络。第一种配置使用一个2.5uF的并联电容器（接地）和一个串联10mH的电感器。第二种则使用相反的配置。我选择了后者并将其添加到模拟图中（见图5）。你可以仔细检查。我在源侧保留了一个1kΩ电阻，在负载侧保留了4Ω。然后我添加了L1 = 10mH和C1 = 2.5μH。模拟结果显示，负载中的功率从0.197mW增加到12.4mW。记住，这正是我们在完美匹配的1kΩ负载中得到的结果！

也许快速的手动计算会帮助你理解发生了什么。我确信你记得如何计算电感L1和电容C1在1kHz频率下的阻抗，对吗？我们有：

[ Z_{L1} = j \omega L = 2 \pi \times 1kHz \times 10mH \approx 63.4j ]

[ Z_{C1} = \frac{1}{j \omega C} = \frac{1}{j \times 2 \pi \times 1kHz \times 2.5uF} \approx -63.4j ]

如果你考虑源电阻（R1）和电感器（L1），它们是并联的。所以它们的总体阻抗是：

[ Z_{R1 + L1} = \frac{R1 \times Z_{L1}}{R1 + Z_{L1}} = \frac{1k \times 63.4j}{1k + 63.4j} ]

计算一下，你会得到ZR1 + L1 = 4 + 63.4j。看，电阻部分现在是4Ω，如所需，但有一个+63.4j的电感电抗。但是，添加串联电容器会抵消这个电抗，因为ZC1 = –63.4j，我们得到4Ω。是的！

从低到高阻抗

再次强调，这里没有什么魔法。只是基本的电路行为。如果你按照我的建议构建测试电路，使用发生器、1kΩ电阻和4Ω扬声器，我强烈建议你抓住一个10mH电感器和2.5µF电容器（2.2µF也很可能起作用）。将它们添加到电路中，你应该能听到扬声器发出更响亮的信号。

到目前为止，我已经演示了LC网络可以将高阻抗转化为低阻抗，但它也可以反过来工作。在图6中，我以±1V源为例，频率仍为1kHz，内部阻抗为4Ω，并通过正确的LC匹配网络将其连接到220Ω负载。结果，模拟显示它确实有效。输出功率为31.4mW，这是可能的最大值。你可以自己检查。这可能看起来不奇怪，但再看看图6，关注波形。匹配网络之后，电压几乎是±4VPP。这比输入电压±1V要高。没有其他电源。电路完全是无源的。这意味着这种从低到高阻抗网络实际上在增加信号电压。这非常类似于升压电压转换器。电感和电容形成一个共振网络，增加电压。当然，电路不会产生任何功率。电压增加，但电流相应减少。

带通问题

如前所述，这样的LC匹配网络仅在单一频率下工作。当我计算部件值时，我在频率框中输入了“1kHz”。如果输入信号的频率不再是1kHz，这个网络会发生什么？我让QUCS为我计算了这个问题（见图7）。如预期的那样，输出功率在单一频率（这里是1kHz）下最大，当频率偏离此值时功率会下降。更确切地说，这样的LC匹配网络有一个质量因子Q，决定了匹配的带宽。当阻抗不匹配增大时，Q值也增大，带宽变窄。

如果你阅读关于阻抗匹配网络的书籍，比如参考部分中列出的非常好的书，你会了解到更多复杂的匹配网络可以用不止两个L或C来构建。这些部件可以排列成并联/串联/并联配置（所谓的π网络），或串联/并联/串联（T网络）。然而，可以证明，简单的LC网络实际上是提供更宽频率匹配的网络。所有其他π或T网络将有更高的Q值，因此频率范围更窄。

然而，有技术可以获得更宽的阻抗匹配，但这需要更多的无源部件。最简单的是链式LC方法。如前所述，如果输入和输出阻抗较近，匹配网络的频率响应会更宽。因此，与其使用一个匹配网络将4Ω转换为220Ω，不如使用中间阻抗Z，首先将4Ω转换为Z，然后将Z转换为220Ω。这样两个匹配网络将有更低的Q值，比单一网络更宽的频率范围。最优结果将通过输入和输出阻抗的几何平均值来计算，这里是4和220Ω，分别计算得到Z ≈ 30Ω（即√800）。我计算了两个匹配网络，从4到30Ω，然后从30到220Ω。模拟结果显示在图8中。如果你将其与之前的版本进行比较，你会看到总体输出功率相同，但在频率范围内匹配更宽。当然，使用两个以上的阶段是可以的，你会得到更宽的匹配。不要犹豫，下载QUCS并自行测试。

自己试试

到此为止。为了尽可能保持简洁，我只讨论了纯电阻源和负载，但同样的计算和方法也适用于有反应负载的情况，如天线。我也避免了介绍一个很棒但令人生畏的工具——史密斯图表。这将留到另一篇文章中。

再次强调，您必须相信阻抗匹配实际上既有用又简单。而且，一如既往，最好的方式是亲自尝试。我希望这篇文章能帮助你迈出第一步！享受阻抗匹配的乐趣！

资源

C. Bowick, J. Blyler和C. Ajluni，《阻抗匹配》，收录于J. S. Love的《RF前端——世界级设计》，Newnes/Elsevier，2009年。
G. Breed，“提高简单匹配网络的带宽”，2008年，高频电子学，www.highfrequencyelectronics.com/Mar08/HFE0308_Tutorial.pdf。

来源

Quite Universal Circuit Simulator (QUCS)
QUCS团队 | http://qucs.sourceforge.net/