基于搜索的路径寻找方法（Dijkstra， A*和Jump Point Search）

首飞Kevin

对解空间的定义

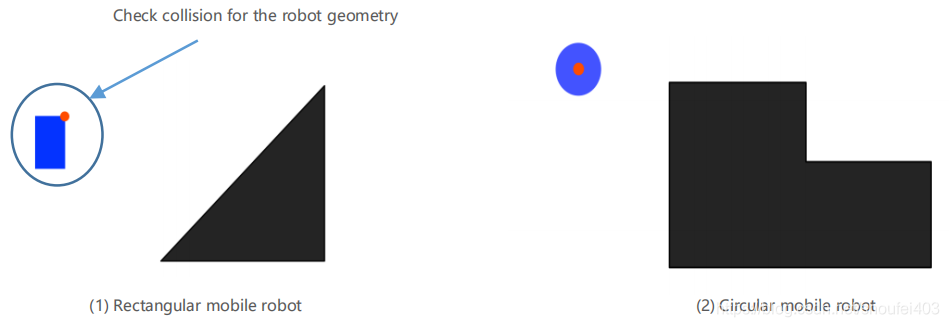
在这里插入图片描述
先看我们会遇到的一个问题。上图描述了在地图中不同机器人的形状和尺寸。因为形状和尺寸的差异让碰撞检测问题变得非常复杂。很自然我们会想能不能仅用一个点来描述机器人呢？忽略掉形状和尺寸的差异。这大大减小了路径寻找的复杂度。所以有了下图描述的解决方案。
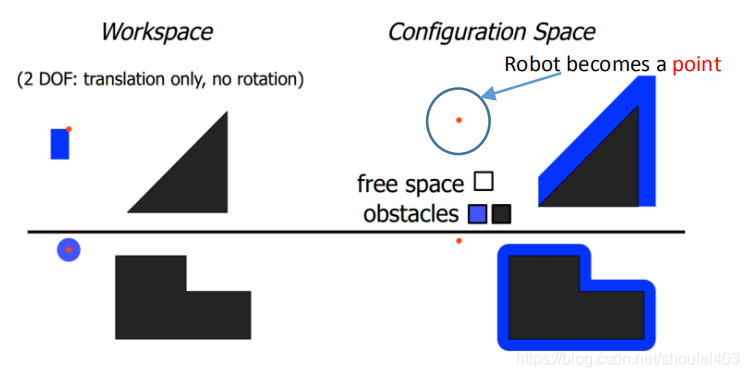
在这里插入图片描述
黑色块为障碍物，包裹在障碍物周围的是根据机器人形状大小生成的膨胀层。对于复杂的机器人形状则通常使用简单的形状去近似。而机器人在地图中就直接简化成一个点了。可以看到机器人形状大小不同，生成的膨胀层也不同。而我们需要寻找的路径就在地图中除了障碍物和膨胀层的自由空间中，也就是解存在的空间。在进行路径搜索前必须先做这样的简化处理。

认识状态空间图

状态空间图的基本概念

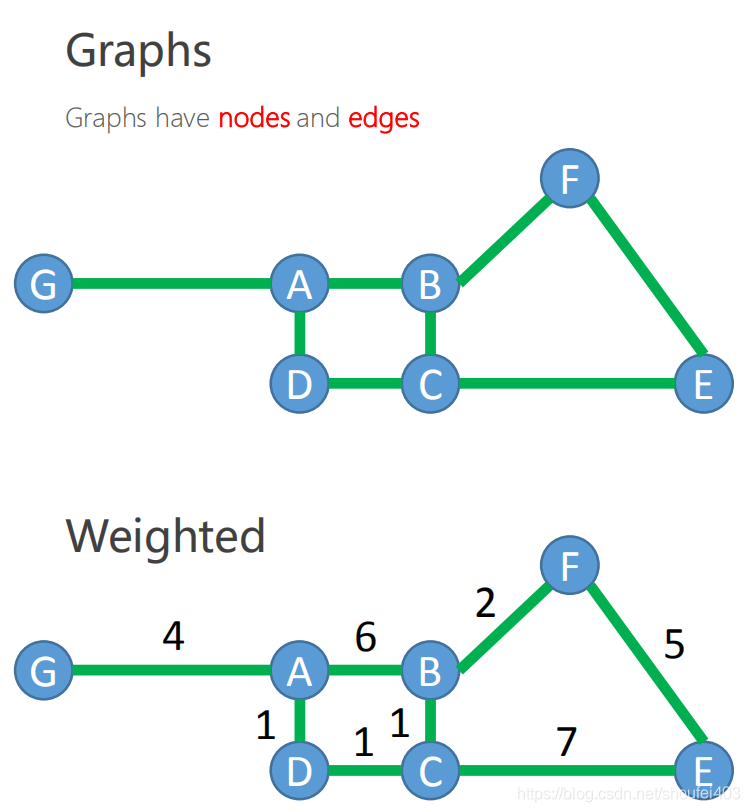
在这里插入图片描述
图通常包含节点和边。对于某些图，其边的代价是一样的。而有些则每条边的代价都不样。而代价值在后面介绍的搜索算法中会有用到。它会参与决定搜索的方向。

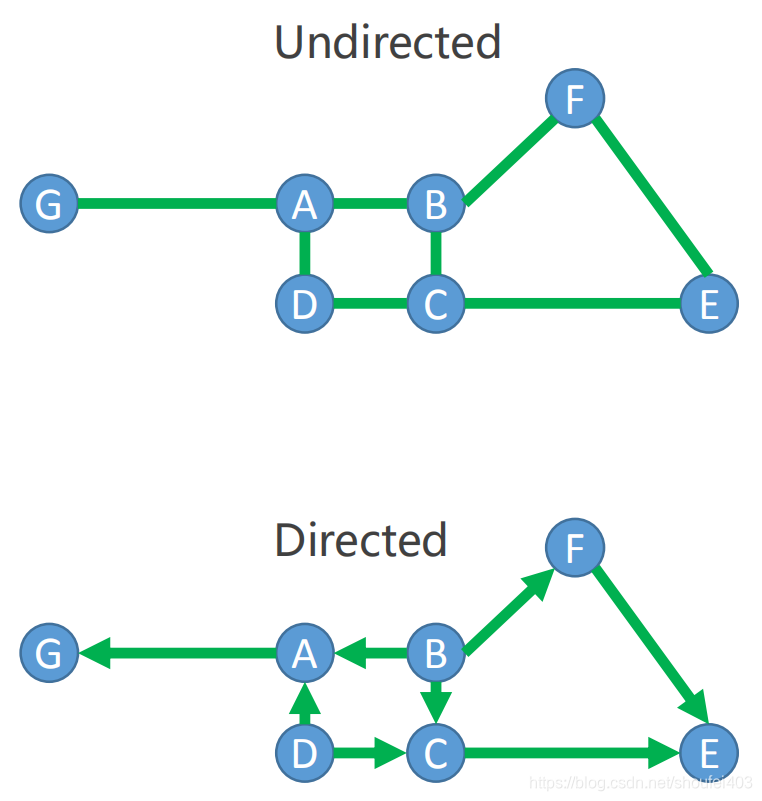
有些图的边存在方向性，有些则不存在。

常见的状态空间图

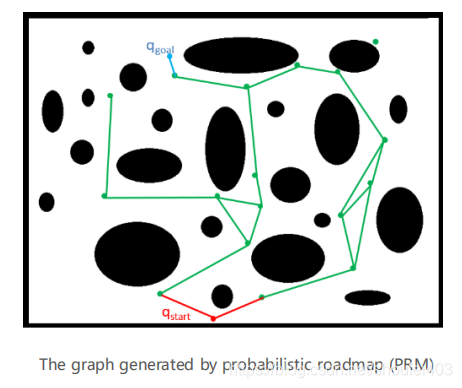
在这里插入图片描述
这是一个通过概率方法生成的图。节点与节点之间的边具有不同的代价值。

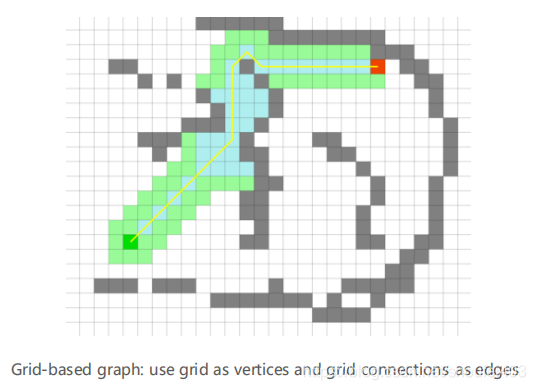
基于栅格的图是本篇文章重点关注的图。每一个栅格就是一个节点。而边就是节点与节点间的连线。

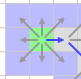
每一个节点有8个搜寻方向。4个对角方向边的代价值为$\sqrt2$，其余邻近的4个方向边的代价值为1。通常它是单向的，扩展了的栅格不会重复扩展。

路径搜寻方法的基本思路

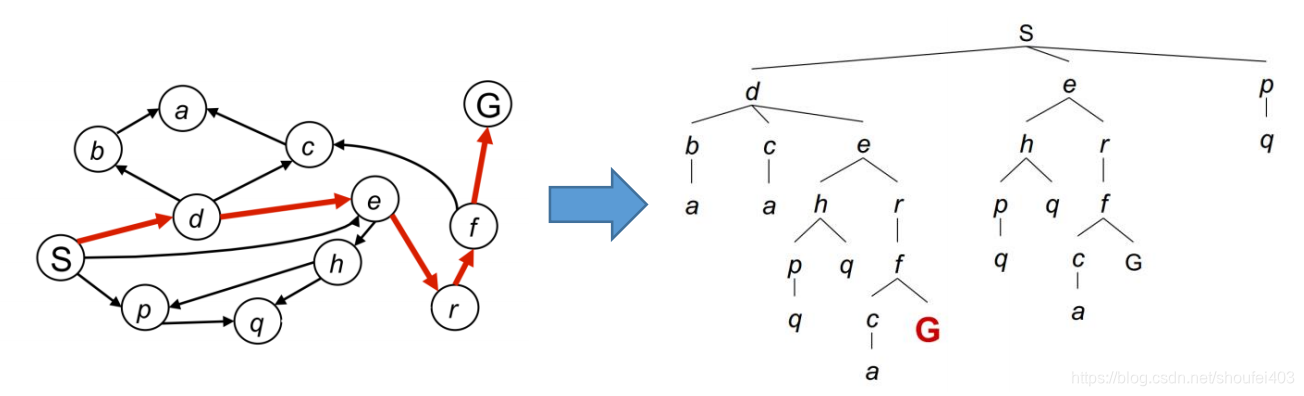
在这里插入图片描述
路径搜索通常是从起点开始构建一个搜索树。但我们不总是将整个树都生成出来。这样树会非常大。路径搜索问题就是想办法扩展更少的节点花费更少的时间来找到目标节点。它通常包含下面几个主要步骤：

以开始节点为根节点初始化一个容器
将扩展的节点添加到容器中
根据得分规则弹出容器中的一个节点
获取该节点的所有邻居节点
把所有邻居节点添加到容器中

重复3~5步骤，直到找到目标节点或者穷尽了容器里所有的节点但仍然没有找到目标节点。需要注意的是，已经从容器中移除的节点是不会再加入到容器的。而整个搜寻算法最关键的部分就是怎么从容器中弹出最合适的节点，从而更快的找到目标节点。

Depth First Search (DFS)

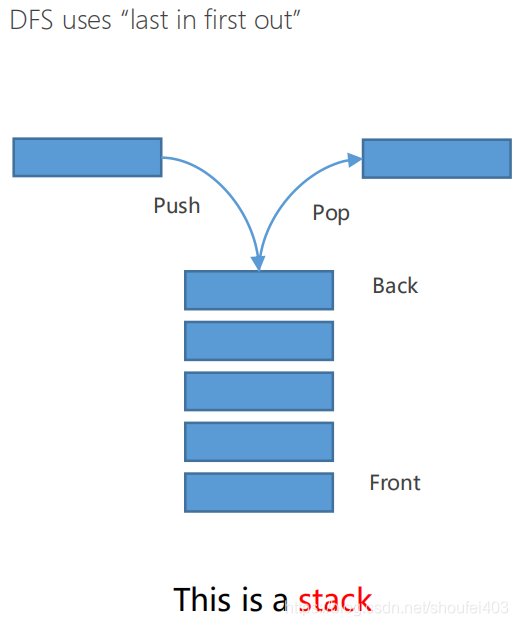
在这里插入图片描述
深度优先搜索其实维护的是一个堆栈结构。

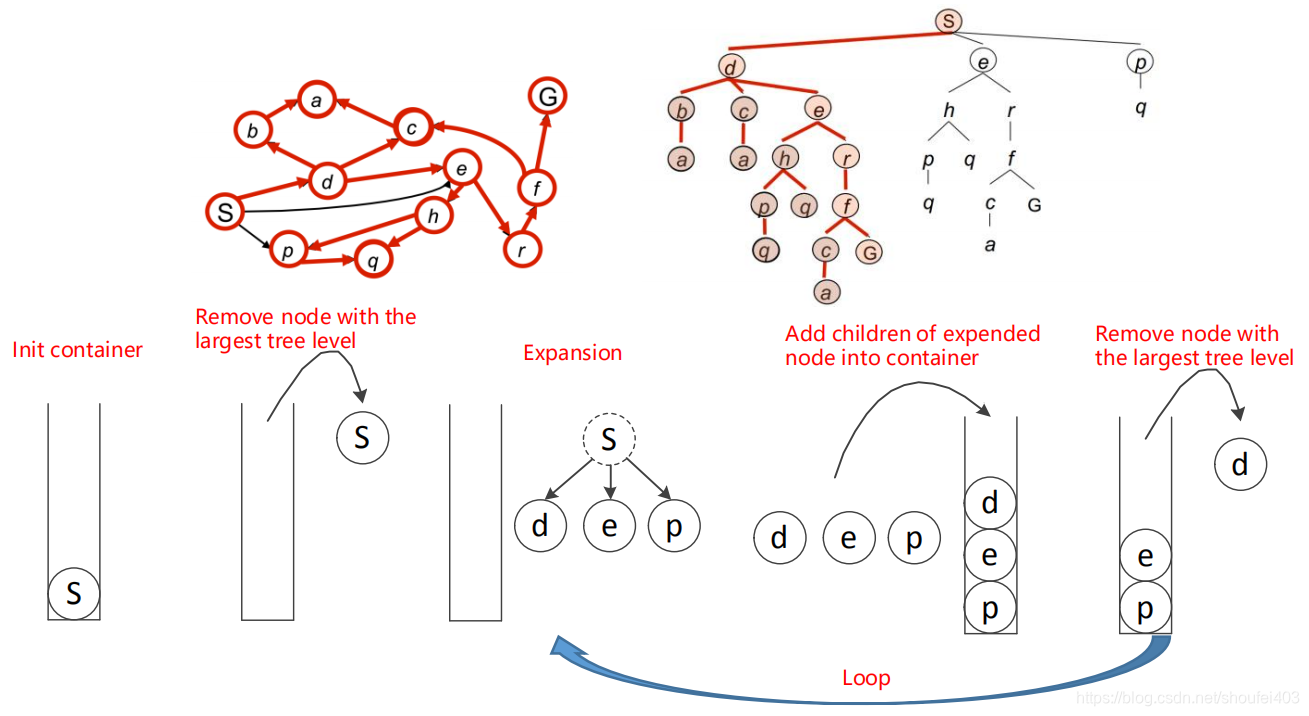
深度优先搜索基本就是一条道走到黑，再回到上一个有分支的节点，走该节点的下一个分支。

Breadth First Search (BFS)

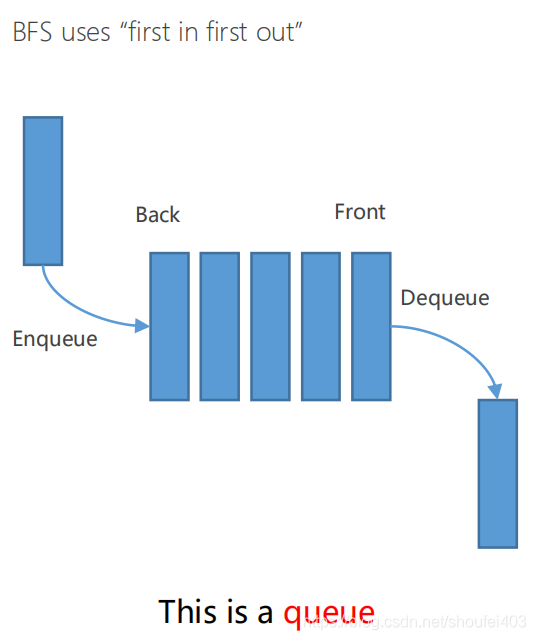
在这里插入图片描述
广优先搜索其实维护的是一个队列结构。

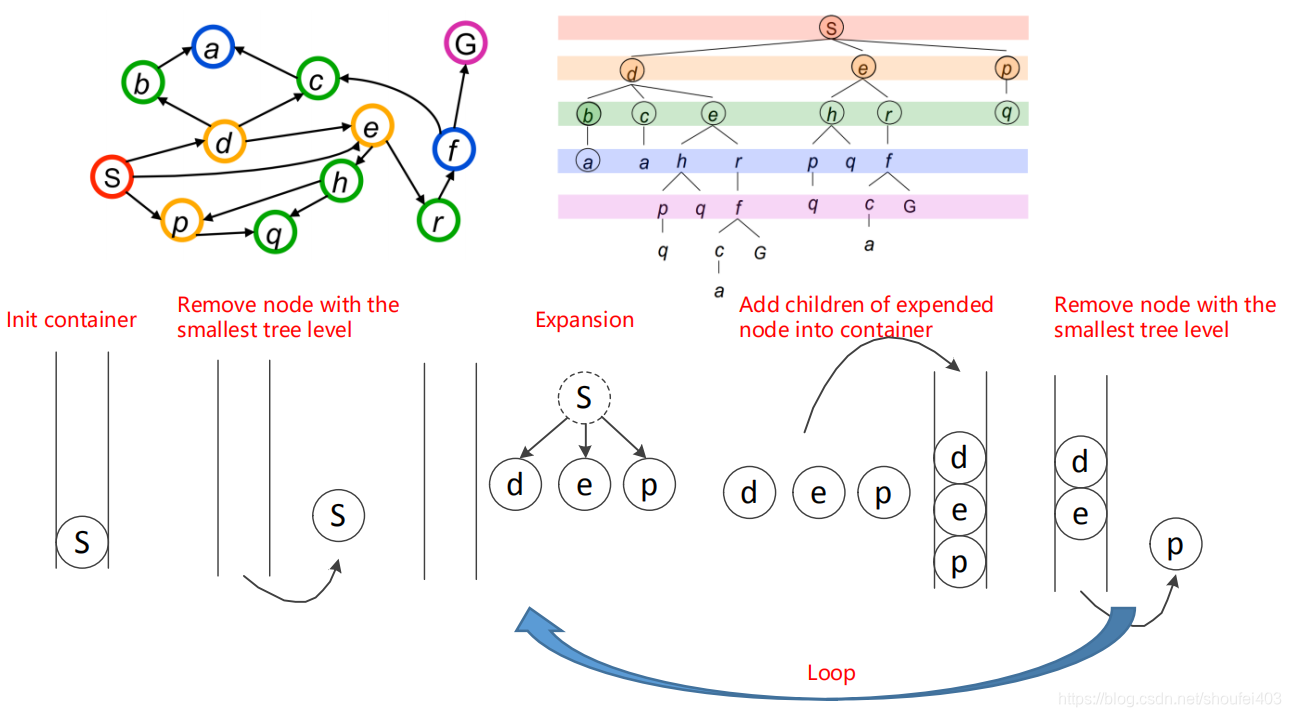
广优先搜索先将同一级的节点压到队列中，上一级的节点处理完后再进行下一级节点的处理。

广度优先搜索总是等可能的向8个方向扩展，最终接触到目标点，输出一条最优路径。深度优先搜索则只能得到次优的路径。所以通常是使用广度优先搜索的方法来寻找路径。

Dijkstra

之前我们说路径搜索的关键是怎么从容器中弹出一个合适的扩展节点。Dijkstra累计计算从开始点到当前节点的代价值，并用g(n)表示。它为容器中的每一个节点计算g(n)值。弹出g(n)最小的节点作为后续扩展的节点。
算法流程：
在这里插入图片描述
Dijkstra使用g(n)来寻找移动代价最低的扩展点。但移动代价低的方向可能不只一个方向，所以它会向多个方向进行搜索。这样其实就花费了更多的时间。

这个图描述了其扩展的方向性。

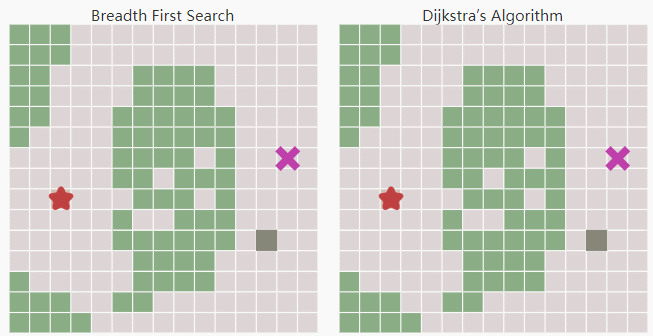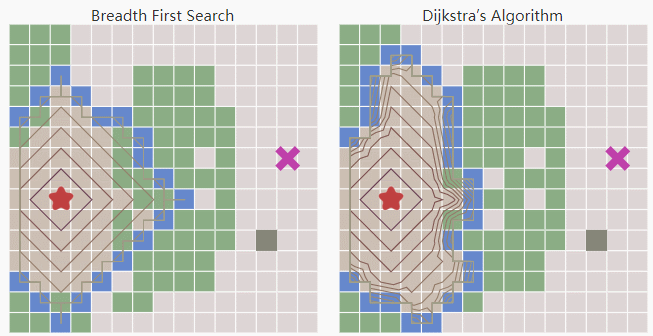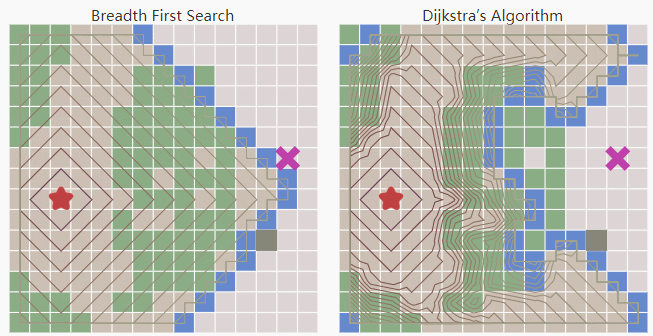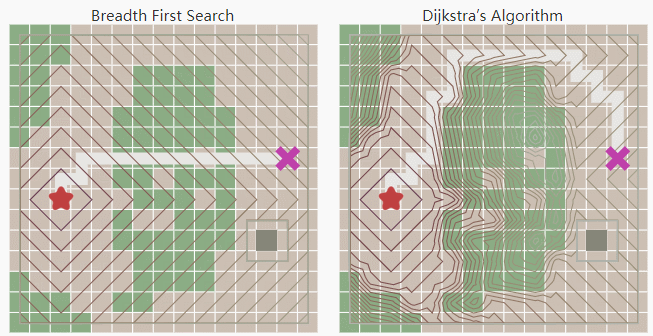
Breadth First Search是按照压入队列的顺序，先入先出来弹出。所以它是均匀的向四周扩展。因为中间绿色的方块的移动代价要高。Dijkstra则生成了一条避开中间绿色方块的路径。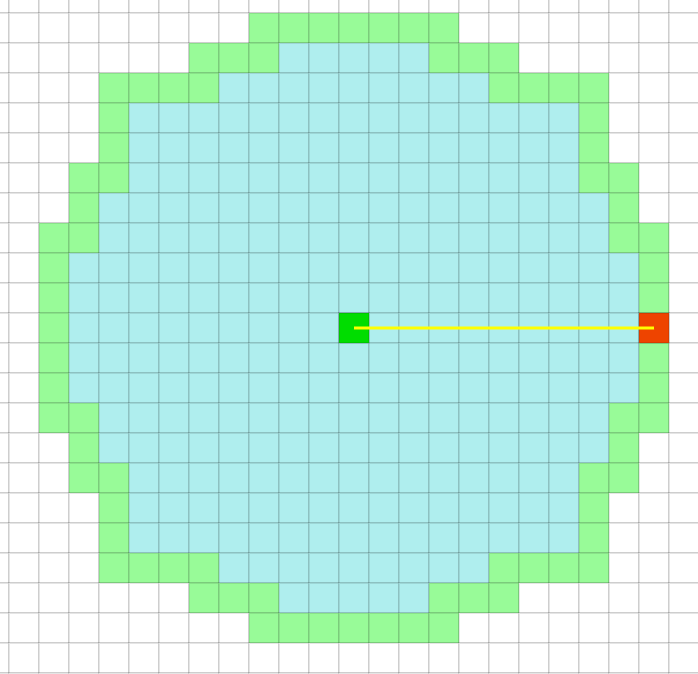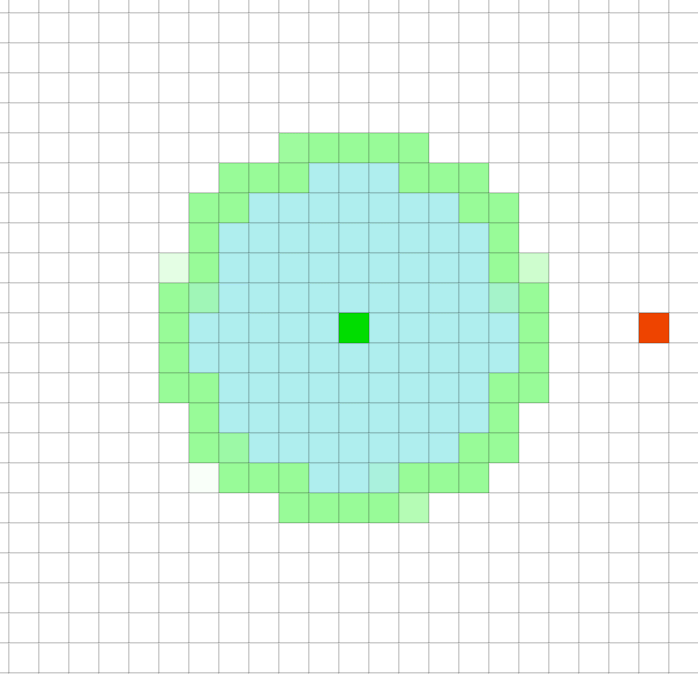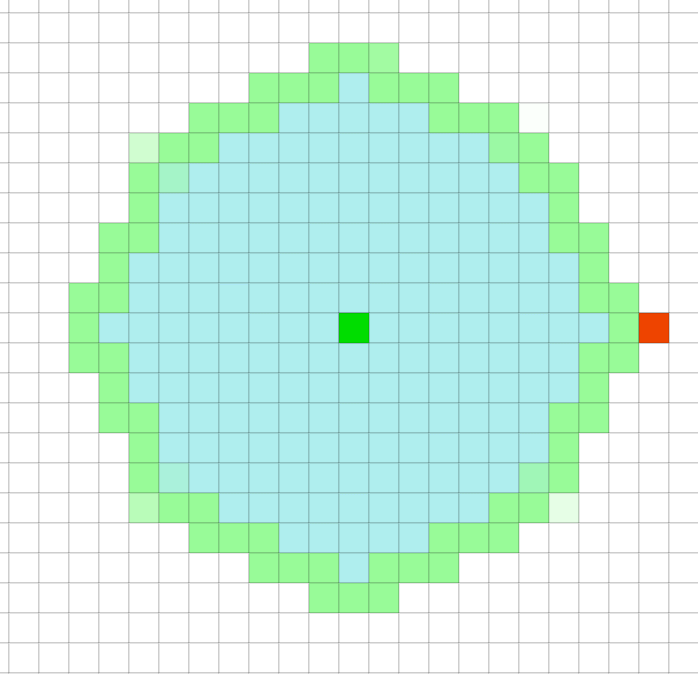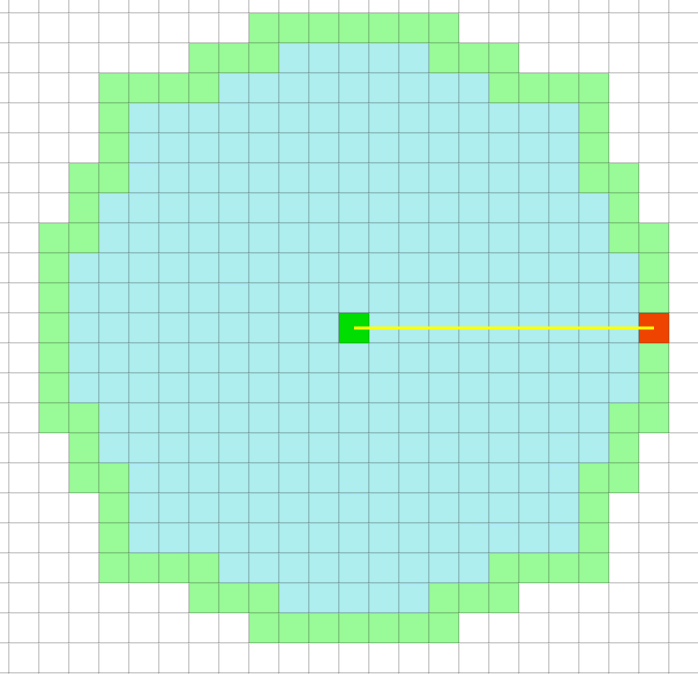

在这里插入图片描述
但对于栅格地图来说，因为每个方块的移动代价是均匀的(即uniform cost search)，Dijkstra仍然是向各个方向均等的扩展。注意这里是允许对角扩展的。

启发式搜索（Heuristic search）

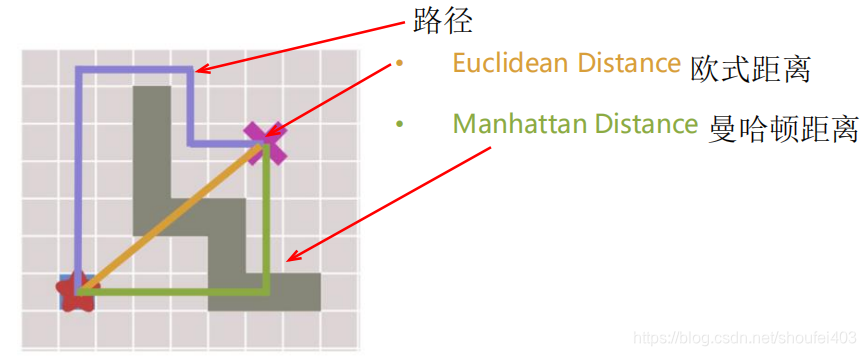
在这里插入图片描述
启发函数的作用就是建立一个规则。通过这个规则对容器中的节点都计算一个得分。对得分进行排序，选出得分最低的节点作为下次扩展的节点。得分的计算有多种方式。尽量选择计算简便的，因为它需要执行很多次。太复杂的启发函数可能影响算法的执行效率。上图中显示了两种常见的启发函数：

欧式距离
曼哈顿距离

贪心算法（Greedy Best First Search）

Greedy Best First Search仅使用启发函数来计算节点得分。弹出容器中得分最小的节点作为扩展节点。
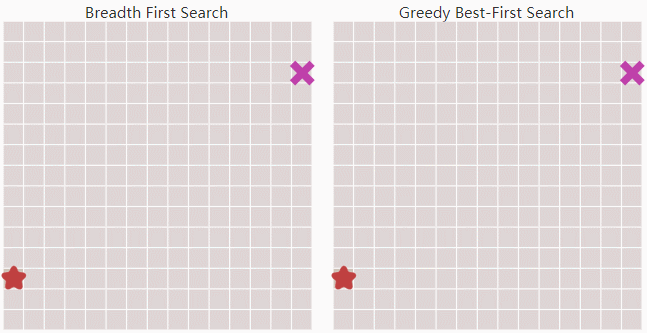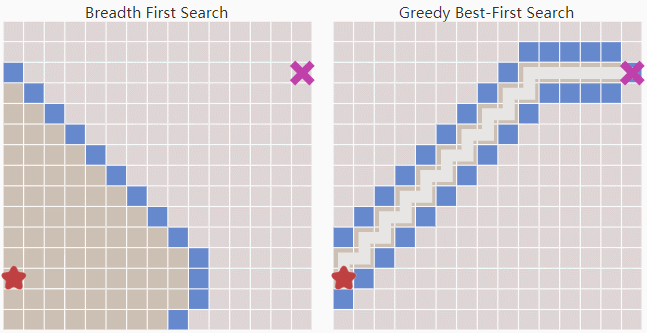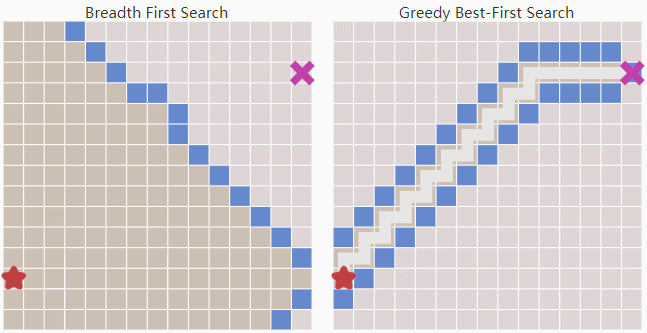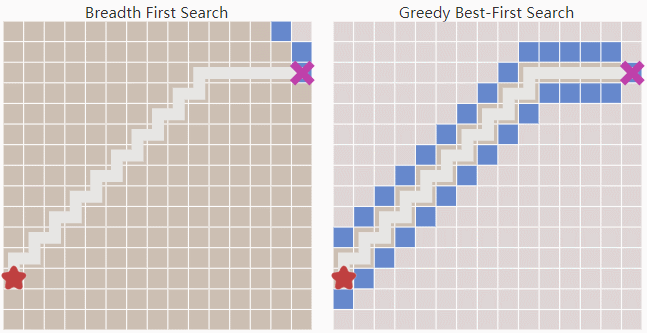
在这里插入图片描述
Greedy Best First Search相对于Breadth First Search有更强的目标导向。启发函数会帮助它找到合适的扩展方向。所以它可以用更短的时间找到目标点。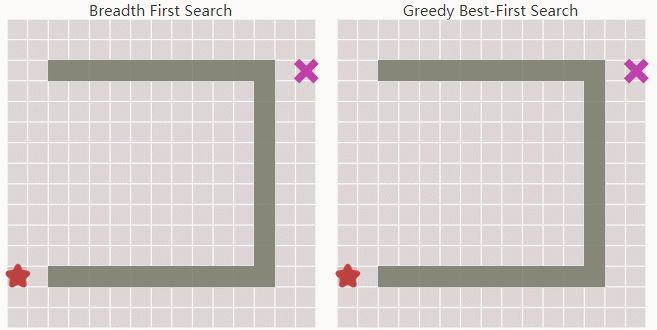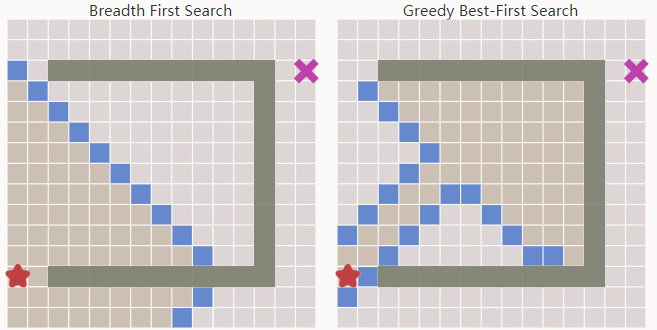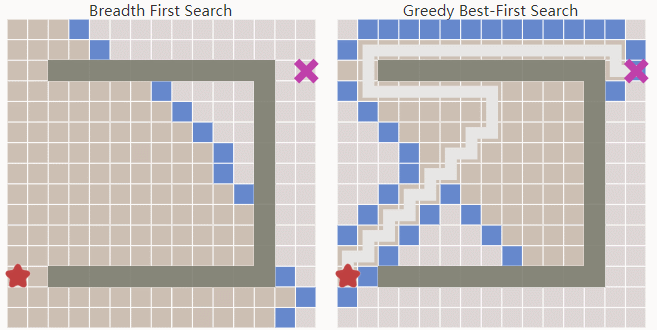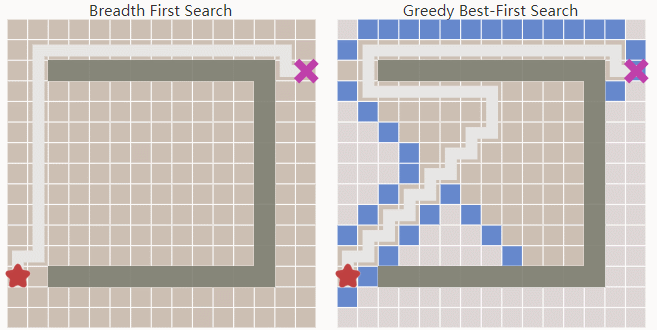

在这里插入图片描述
但Greedy Best First Search在有障碍物的环境中常常不能得到最优解。

A*: Dijkstra with a Heuristic

A* 则在Dijkstra的基础上增加了启发函数。用g(n)表示节点累计的移动代价，用h(n)表示启发函数的计算值。A* 为容器中的每一个节点按照公式f(n)=g(n)+h(n)计算一个得分。每次循环则弹出一个容器中得分最小的节点来扩展。
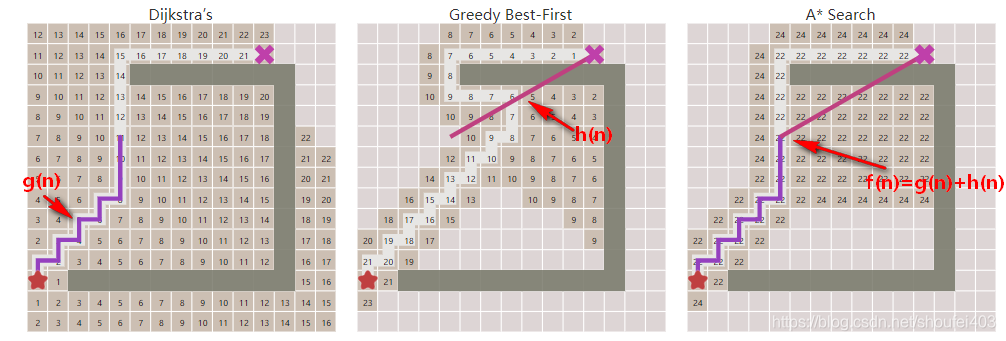
在这里插入图片描述
上图显示了3种算法的主要差异。

A* 的算法流程如下：
在这里插入图片描述
Breadth First Search 和 Dijkstra总是能找到最优的路径，但它们需要花费更多的时间。Greedy Best First Search在有障碍物的环境里不一定能找到最优的路径，但它花的时间相对少。当h(n)的值小于实际节点到目标点的真实距离时，A能找到最短的路径。事实上，当h(n)足够小，A 将慢慢变成Dijkstra；而当h(n)变得足够大，A*将慢慢变成Greedy Best First Search。

工程优化上的考虑

我们希望路径搜索算法只需搜寻必要的节点来生成一条最优路径。但许多路径有相同的$f$值。A* 将等可能的搜寻它们。所以思路应该是尽可能让不同的路径有不同的$f$值。不同的$f$值让A* 搜寻更少的节点。

思路一：使计算的h(n)更贴近实际的距离值
针对栅格地图，使用欧式距离计算的$h$值常常和实际的真实距离相差较远。如果考虑栅格对角线的距离，使用下面的公式计算$h$值，效果会有所改善。

$d x=a b s(\text { node. }x-\text { goal. } x)$
$\mathrm{d} y=\operatorname{abs}(\text { node. } y-\text { goal. } y)$
$h=(d x+d y)+(\sqrt{2}-2) * \min (d x, d y)$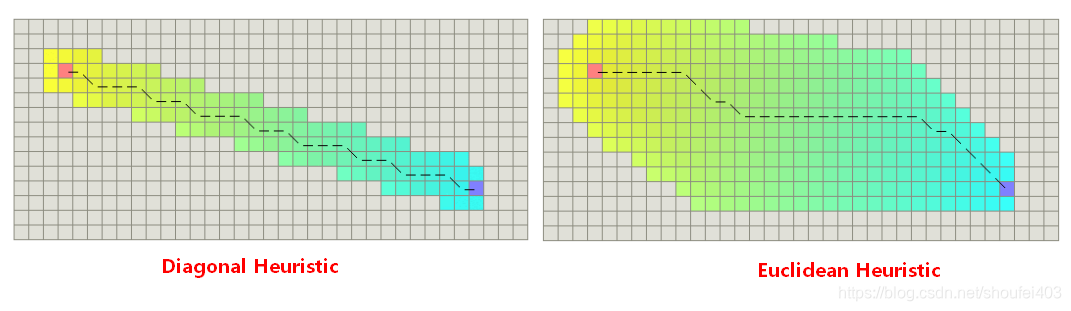

在这里插入图片描述
思路二：轻微打破h(n)需要小于实际的距离值的规则
使用下面的公式计算$h$值。

$p<\frac{\text { minimum cost of one step }}{\text { expected maximum path cost }}$

$\mathrm{h}=\mathrm{h} \times(1.0+\mathrm{p})$
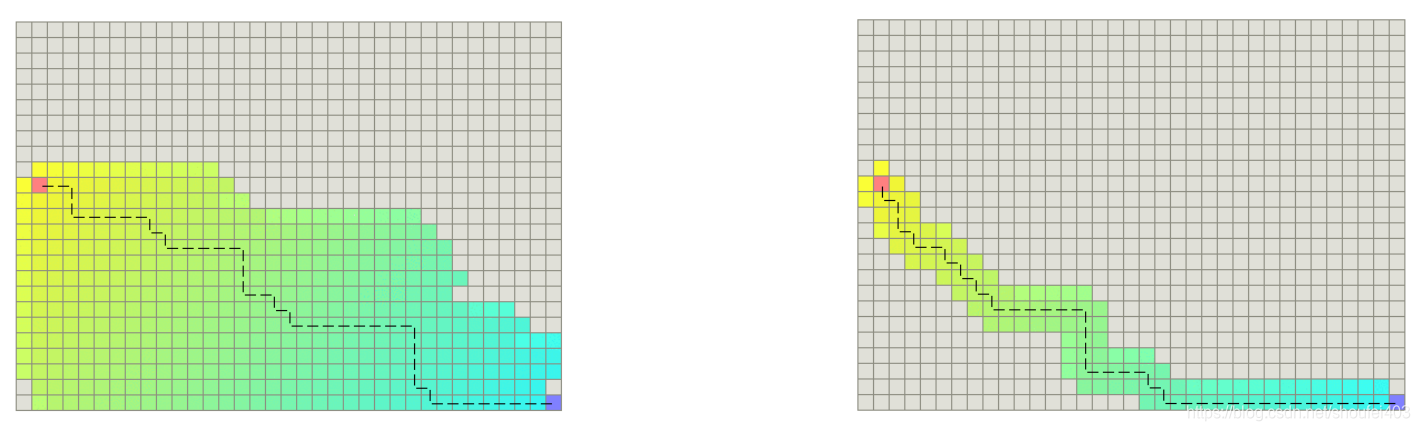
在这里插入图片描述
右边为使用了该方法进行改善所呈现的结果。

思路三：当有相同的$f$值时，则比较$h$值

Jump Point Search

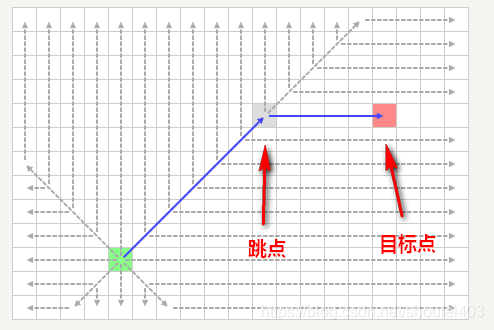
Jump Point Search方法主要被应用于移动代价均匀的栅格地图（uniform-cost grid environments）。在这样的地图中比较容易出现$f$值相等的路径。这样就导致其搜寻的节点增多，来回在$f$相等的节点间跳动，消耗了更多的时间。Jump Point Search则制定了一系列的规则来寻找跳点(Jump Point)，并将这些跳点加入到容器中。相比A等可能地扩展对称路径的所有节点，Jump Point Search只会扩展特定的几个节点，大大减少了搜寻路径的时间。

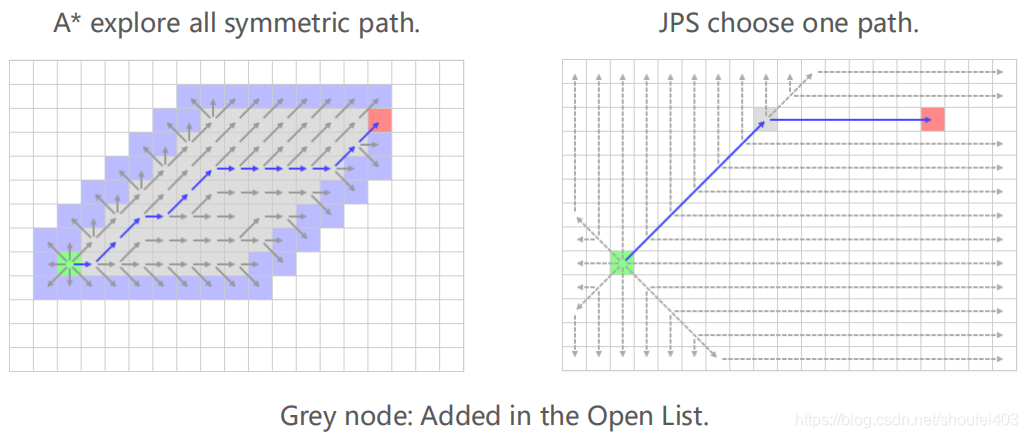
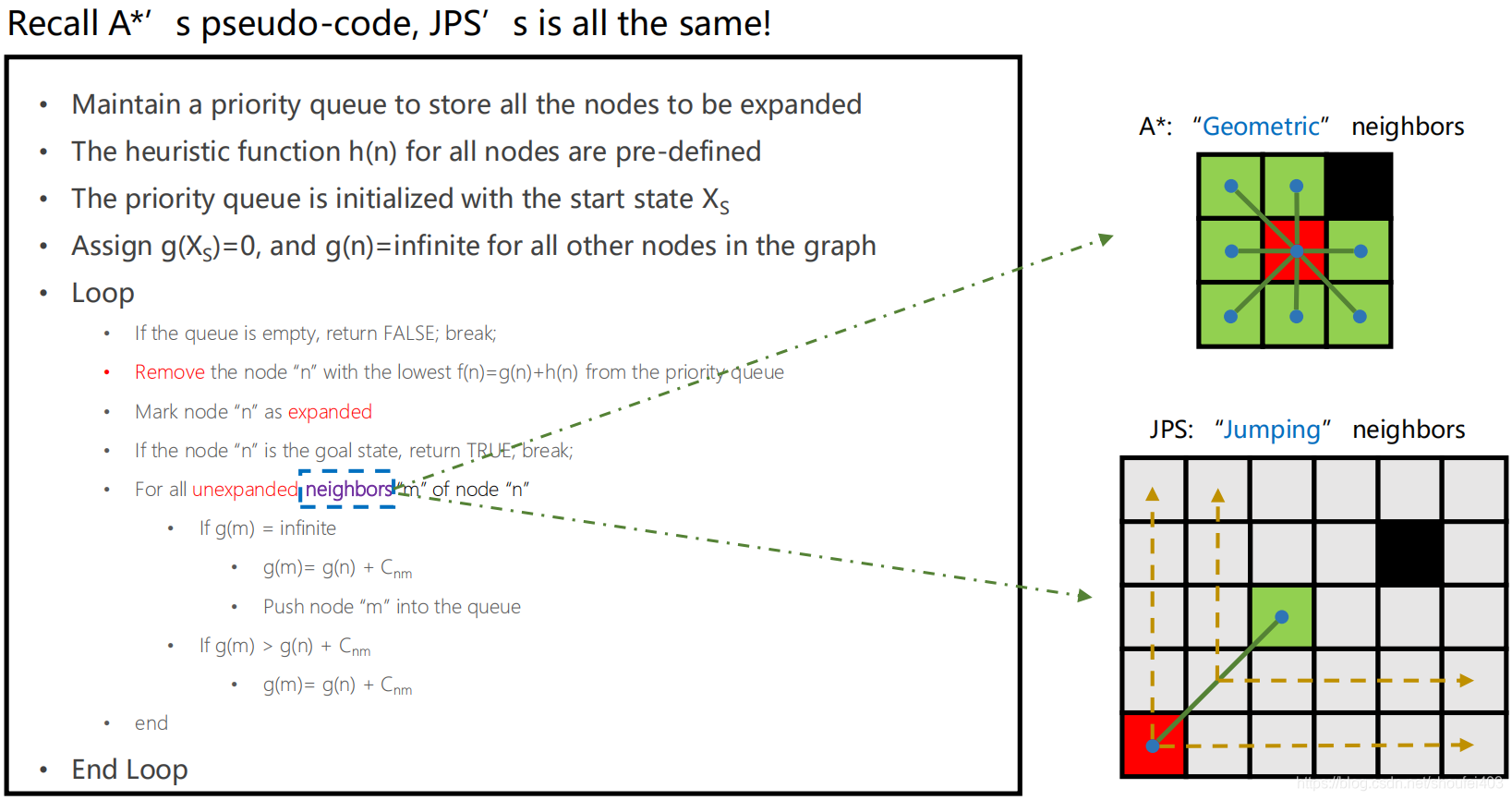
A 和JPS的代码流程上几乎是一样的，只是在扩展节点的方式上有差异。A* 将当前节点几何邻近的所有非障碍物节点都加入了容量中，JPS则只选择特定的几个节点（跳点）加入。

选择跳点的规则

跳点搜索是先进行水平和垂直方向的搜索，再到斜对角方向行进一步，然后再次进行水平和垂直方向的搜索。重复上述步骤，将搜寻的跳点加入到容器中。

Neighbor Pruning
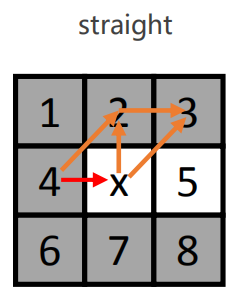
在这里插入图片描述
注意：灰色为不考虑的搜寻方向，白色是将要搜寻的方向

对于水平搜寻和垂直搜寻，其搜寻路线均可用上图描述。针对1，2，6，7栅格，它们都可以不经过x栅格到达，并且移动代价会比经过x栅格更低。所以不考虑从这些栅格扩展。4栅格是已经搜寻过的栅格也不考虑。从4栅格到达3，8这两个栅格均有两条路径，并且移动代价相等。为了简化，认为它们经由2，7栅格到达更优，不必经过x栅格到达，所以也不考虑搜寻。最后就只剩下5作为搜寻方向。

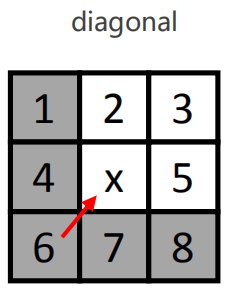
在这里插入图片描述
注意：灰色为不考虑的搜寻方向，白色是将要搜寻的方向

对角线方向的搜寻的情况也和水平垂直方向搜寻类似。通过x栅格再到达1，4，7，8栅格的移动代价会更高。所以不考虑通过x栅格到达这四个栅格。6栅格是已经搜寻过的栅格，这里也不考虑。

Forced Neighbors
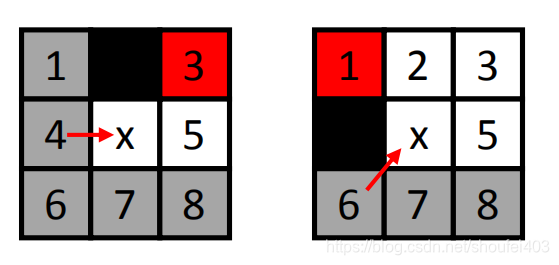
在这里插入图片描述
注意：图中黑色方块为障碍物，红色方块为Forced Neighbors，灰色为不考虑的搜寻方向，白色是将要搜寻的方向。

Forced Neighbors栅格是必须要通过x栅格才能到达的栅格。上图中，因为障碍物的遮挡红色栅格必须要经过x栅格才能到达。此时x栅格就是跳点(Jump Point)。需要将其加入到容器中。

另外，看到目标节点的效果和发现Forced Neighbors栅格是一样的。都需要将对应的栅格认为是跳点，加入到容器中。
在这里插入图片描述

JPS优劣分析

JPS在大多数时候都是效果更好的。特别是在障碍物较多的场景。因为可以更快找到合适的跳点，而不用去搜寻大片没有障碍物的区域。但在较为空旷的环境里，因为需要花费更多的时间搜寻跳点，整体的效果就下来了。
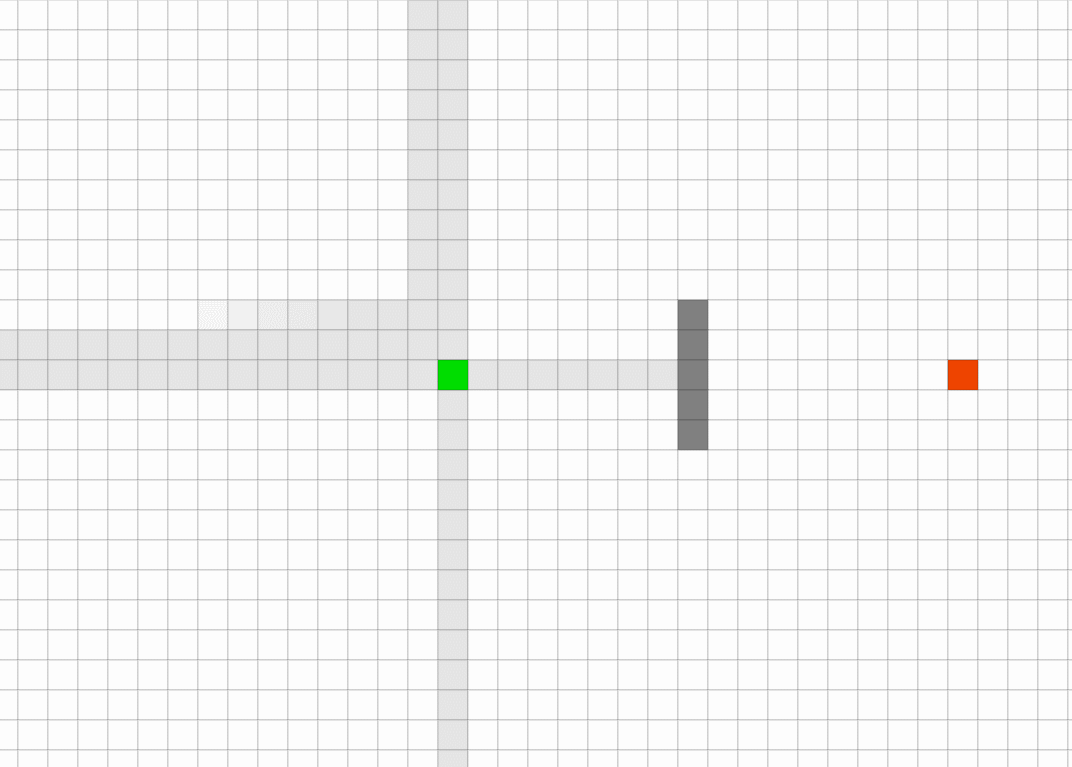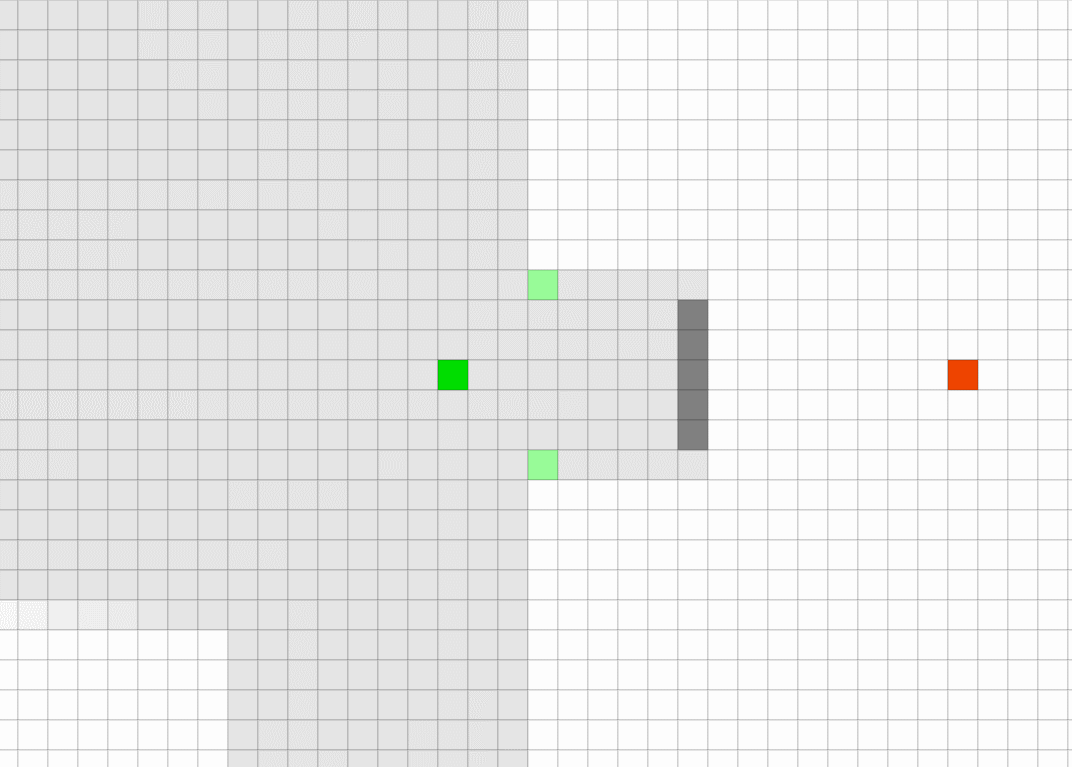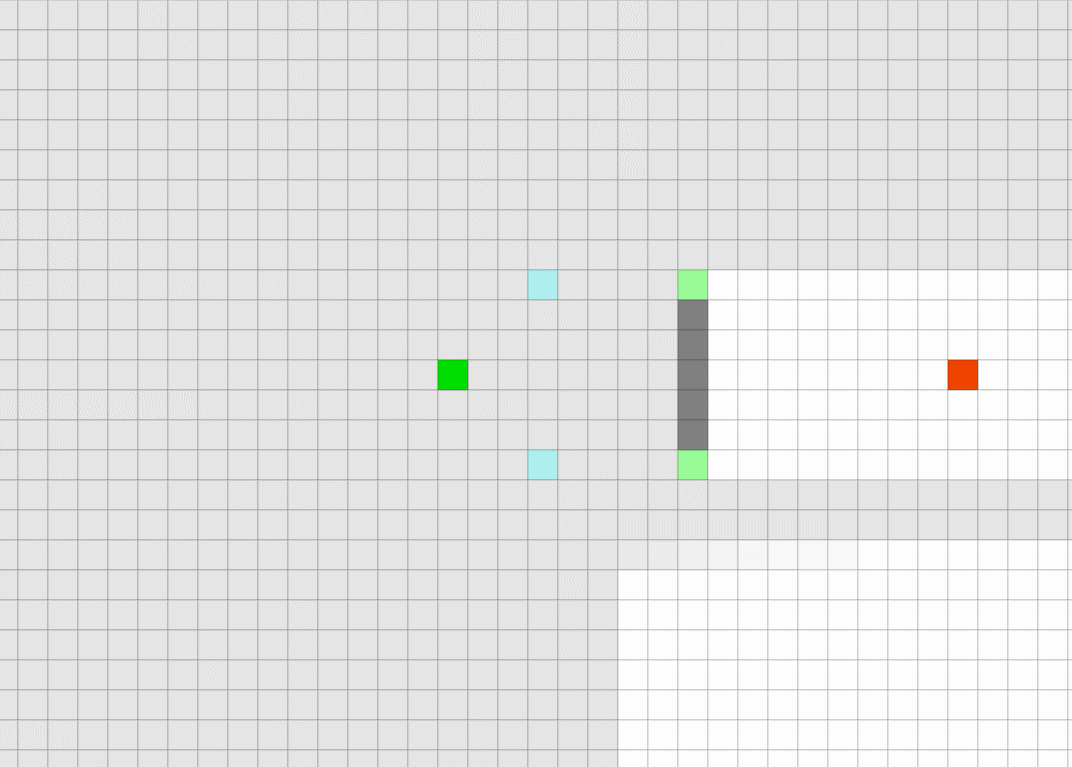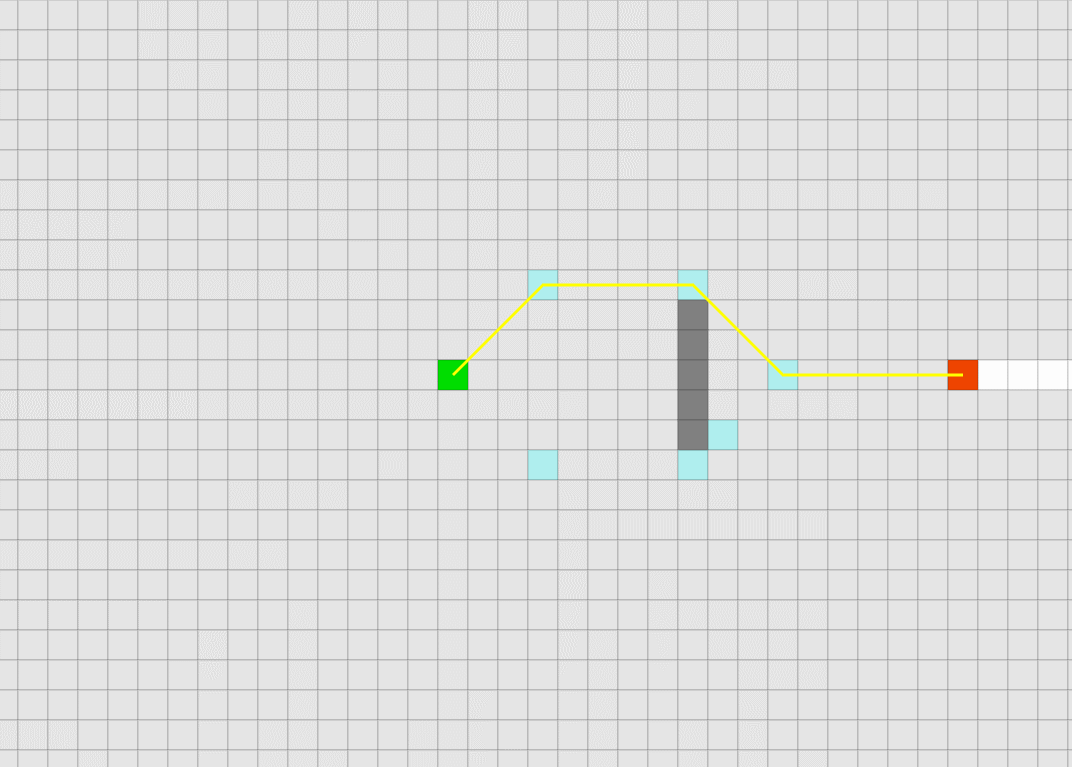
在这里插入图片描述
JPS算法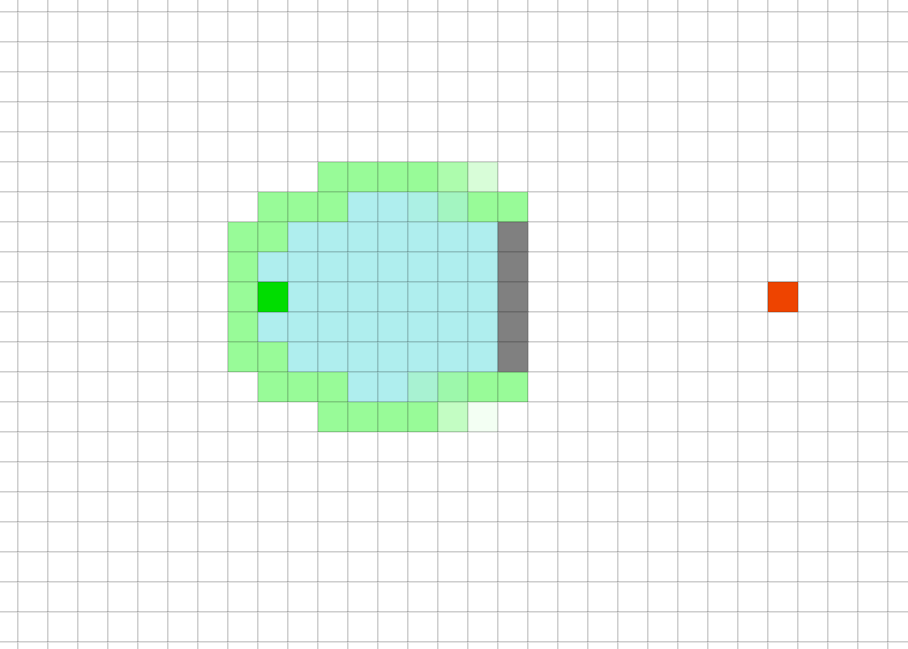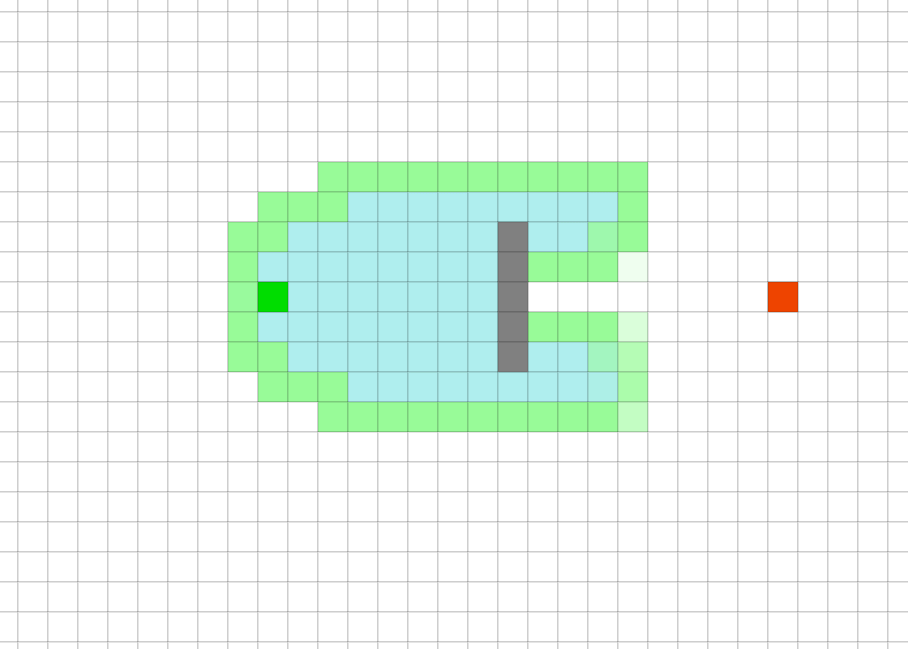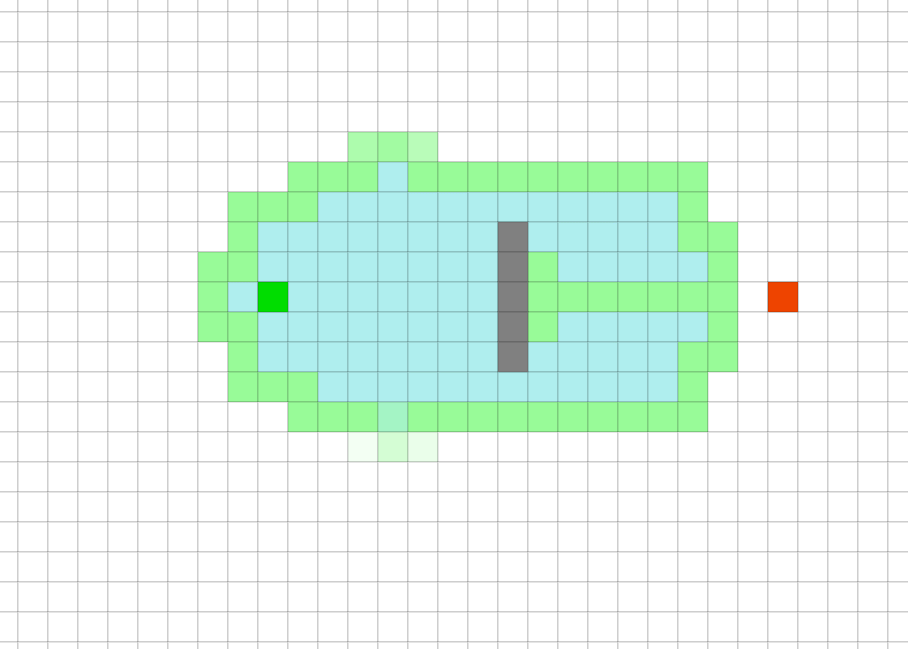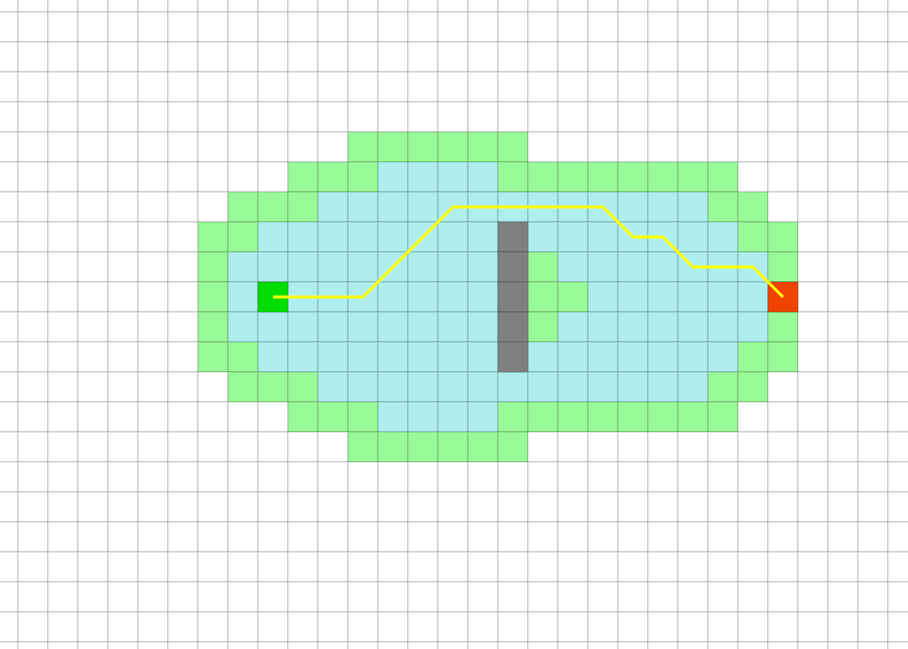

在这里插入图片描述
A*算法

另外，JPS常常用在移动代价均匀的栅格地图里，在其他类型的地图里是不适用的。

https://zerowidth.com/2013/a-visual-explanation-of-jump-point-search.html这篇文章详细介绍了寻找Jump Point的各种规则
参考论文：http://users.cecs.anu.edu.au/~dharabor/data/papers/harabor-grastien-aaai11.pdf

参考材料

吐血推荐Amit Patel讲解A*的博客：https://www.redblobgames.com/pathfinding/a-star/introduction.html
http://qiao.github.io/PathFinding.js/visual/这里可以运行各种路径搜索算法，对比效果。
Daniel Harabor的发布的论文地址