运动学1----绪论和空间
-
我们开始学习运动学的知识,这是后面表达位姿(位置和姿态),线速度,角速度,力和力矩的基础
我参考的书籍如下:
《机器人学导论》

《现代机器人学》

《机器人建模和控制》

《机器人学建模规划与控制》
课程链接:
台大机器人学之运动学——林沛群
https://www.bilibili.com/video/BV1v4411H7ez?spm_id_from=333.337.search-card.all.click
【中英字幕】现代机器人学 | Modern Robotics
https://www.bilibili.com/video/BV1KV411Z7sC?spm_id_from=333.337.search-card.all.click&vd_source=2cb00bb72c9b0db721c2c6945444f148
建议可以翻墙的同学直接在coursera上看原版,b站上的少了很多东西
https://www.coursera.org/specializations/modernrobotics
ME331-机器人建模和控制
https://space.bilibili.com/499858787/?spm_id_from=333.999.0.0
这几个课程互相补充,但是这几个讲的矩阵部分都不是太好,毕竟这门课的先修课是线性代数,刚体力学,反馈控制
所以我推荐mit的线性代数
https://www.bilibili.com/video/BV1ix411f7Yp?p=2&vd_source=2cb00bb72c9b0db721c2c6945444f148学习完这个再来看这个就很有体会了
ok,教材确定下来了,我准备按照下面这几个大纲去给大家说明这运动学是怎么个一回事:
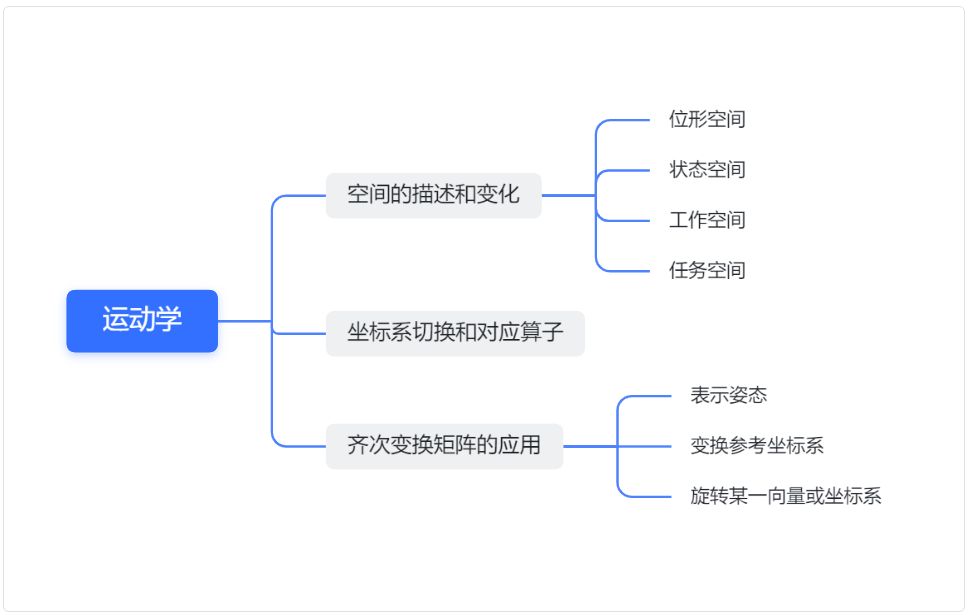
怎么计算自由度有机会可以填一下坑。
位形空间:
With this assumption, Chapter 2 focuses on representing the configuration
of a robot system, which is a specification of the position of every point of the
robot. Since the robot consists of a collection of rigid bodies connected by
joints, our study begins with understanding the configuration of a rigid body.
We see that the configuration of a rigid body in the plane can be described
using three variables (two for the position and one for the orientation) and the
configuration of a rigid body in space can be described using six variables (three
for the position and three for the orientation). The number of variables is the
number of degrees of freedom (dof) of the rigid body. It is also the dimension
of the configuration space, the space of all configurations of the body这里是摘自现代机器人学的书籍
http://hades.mech.northwestern.edu/images/8/81/MR-largefont.pdf
https://www.cnblogs.com/21207-iHome/p/7756084.html
暂时还没有公式插入,就先截图了~~当然这个表达还有隐式表达和显式表达:
假设我们想在一个圆上表示一个点。我们可以通过选择从圆心到所选零角的点从 0 到 2π 变化的角度来做到这一点。两个坐标减去一个约束,为我们提供了圆所属的一维空间。这称为 C 空间的隐式表示,与使用最少坐标数表示空间的显式表示相反:
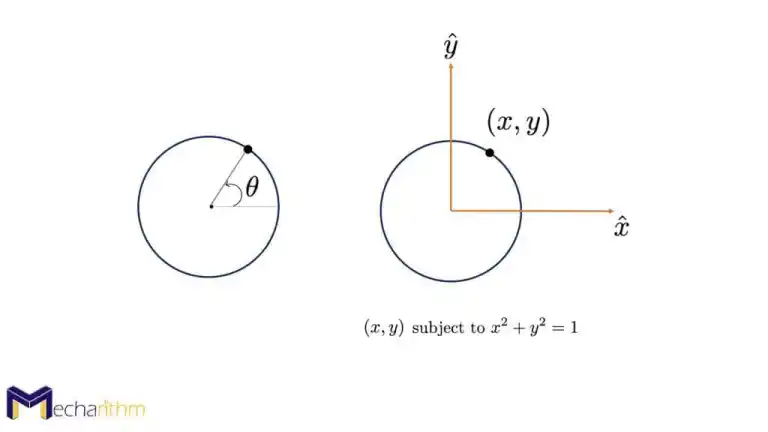
就是对于某个对象,该对象的所有的点及其点能达到的地方的集合,就是位形空间。看二维SE(2),如果x,y,θ三者可以任意取,那其实就是覆盖了整个二维空间,想象一个极坐标系在不停的移动和旋转。
但是理论上是假设了整个空间没有障碍物,物体没有形状。但在实际控制机器人时就必须考虑其真实尺寸,这时机器人就不能被简单地当做一个点。
那我们考虑怎么将一个有形状,有障碍的对象转化成一个点,并描述其位形空间?
那么位形空间就会被工作空间障碍分为自由空间 C (free) 和障碍 空间 C (obs ),其中C = C (free) ∪ C (obs )。关节限制被视为 配置空间中的障碍。
借助C (free) 和C (obs的概念),路径规划问题 简化为在障碍C (obs)中为点机器人寻找路径的问题。
路径规划的目标是在 工作空间中找到一条从初始位置到目标位置的路径,避免所有与障碍物的碰撞。这是一个很难在物理空间中可视化和解决的问题 ,尤其是当维度变大时。但在位形空间中,问题很简单。
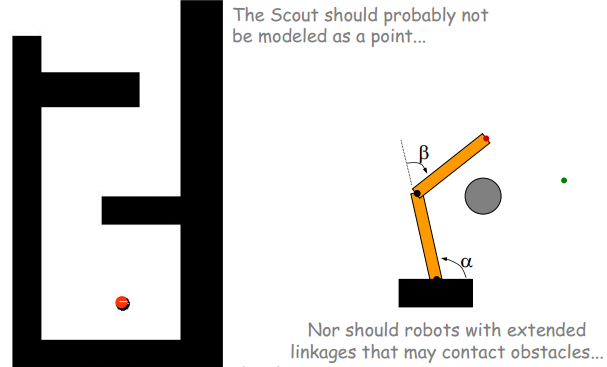
如果机器人不是一个点怎么办?
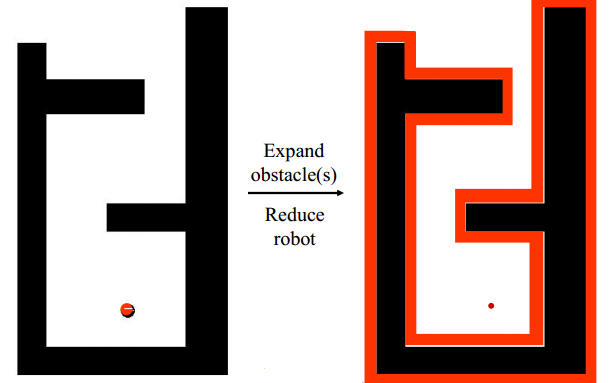
对平面机器人来说,C-Space就是以机器人的尺寸为基础,对工作空间进行一定的膨胀即可得到:
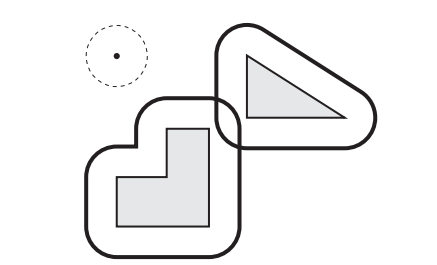
如果对工作空间中的障碍物进行膨胀产生了重叠的部分,如下图所示,则表示机器人不能通过那个区域:
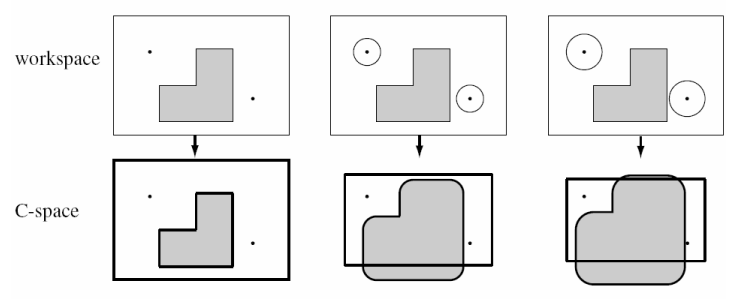
C-Space与机器人实际形状和尺寸有关,从下图可以看出中间和右边两个机器人由于尺寸(直径)太大而不能通过工作空间的某些区域:
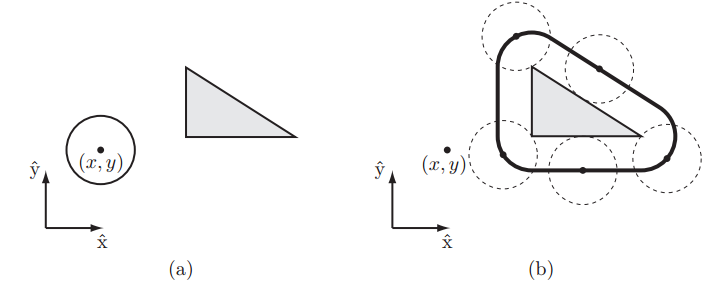
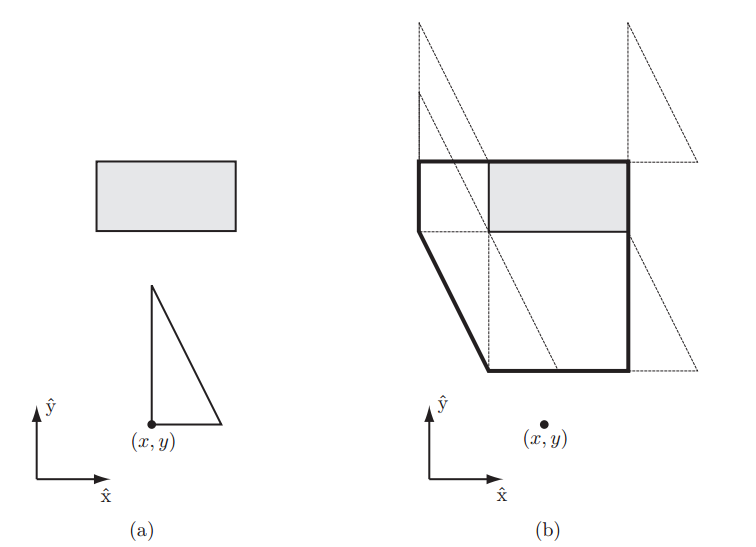
另外机器人的形状也会影响C-Space。下图中的直角三角形代表一个三角形状的机器人,只能在平面内平移,其参考位置点在图中的(x,y)处。灰色矩形是工作空间内的障碍物,将机器人贴着障碍物边界滑行一圈,追踪参考点的位置可以画出一个黑色粗线框的多边形区域。这个区域就是该三角形机器人C-Space中的障碍区域。
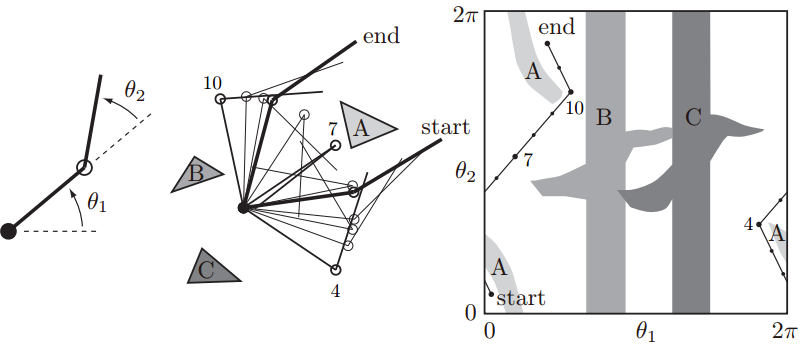
下面是一个关节型机器人的例子。平面二连杆机器人有两个自由度,可以绕两个关节分别旋转0-360°,中间的图描绘了在工作空间中机器人从初始位置开始经过一系列中间点避开障碍物A、B、C运动到目标位置。右图是与之对应的C-Space中的情形:
注意θ(1 )= 0和θ(1 )= 2π(θ(2 )= 0和θ(2 )= 2π)其实是一个角度,因此上面C-Space的左右边界和上下边界其实是连在一起的。其拓扑结构是一个圆环面(torus),正方形构型空间可从圆环面的θ(1 )= 0、θ(2 )= 0处切开、展平得到。
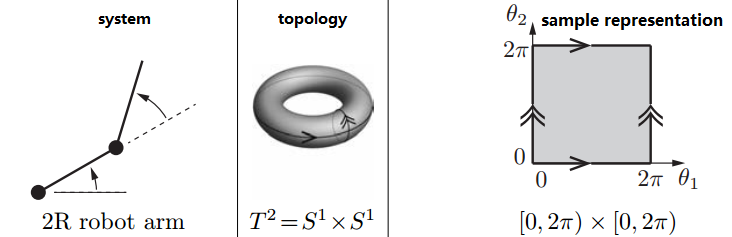
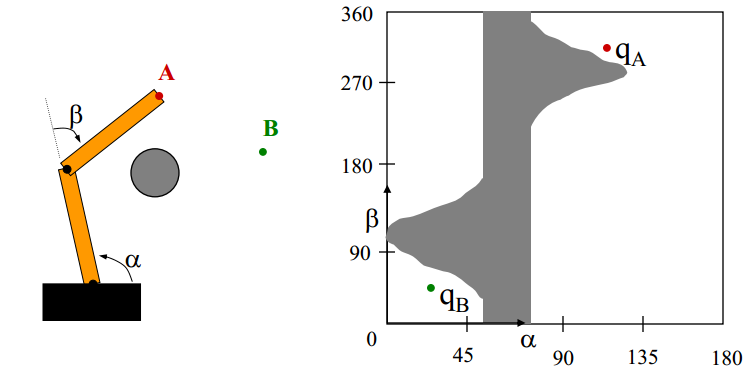
任何落在C-obstacle中的点都表示位于该构型时机械臂与障碍物发生了碰撞。C-Space中从start到end的路径代表了一条工作空间中无碰撞的路径。注意障碍物将C(free)分隔成了三个连通区域,且起点和终点处于同一连通区域中。然而下图这种情况,起始状态q(A)和目标状态q(B)分别位于不连通的区域内,机械臂从A运动到B无论怎么走必然会撞到障碍物。
这是一个能够仿真出位形空间和工作区间的关系的小工具:
https://www.cs.unc.edu/~jeffi/c-space/robot.xhtml

绿色的就是一个小机械臂,红色就是障碍区域,右边的横纵坐标是两个角度(双两杆)。对于任意的一个机械臂,只要画出其位形空间,那么就可以进行路径规划的算法来进行关节空间的运动规划。
这里有个文章讲路径规划的还可以
https://zhuanlan.zhihu.com/p/390698211
如果想进一步学习关于位形空间和路径规划:
https://blog.csdn.net/huangjunsheng123/article/details/118554490
https://www.bilibili.com/video/BV1bp4y1z7mi?p=2&vd_source=2cb00bb72c9b0db721c2c6945444f148任务空间:
任务空间是对机器人任务的空间描述,和机器人无关,比如说任务是机器人写字,那就是写字的这整个平面空间,如果是机器人踢球,那任务空间就是整个球场,这个是和机器人无关,指的是任务的一个空间描述
工作空间:
机器人的工作空间就是指末端能够到达的区域,这个和机器人的机构有关状态空间:
位形是对机械臂的几何结构提供了一个瞬态的描述,而状态空间则是与机械臂的动态响应有关,状态空间是指所有的可能的状态的集合。
机器人的状态变量是指这样的一组变量:结合机械臂的动力学描述,以及未来输入,足以确定机械臂未来的时域响应。 -