运动学2---坐标系变换
-
这一章节主要提纲如下:
一、刚体位姿描述
如何描述刚体:
首先我们是针对三维的物体,那我们就用常见的直角坐标系去描述一个刚体,
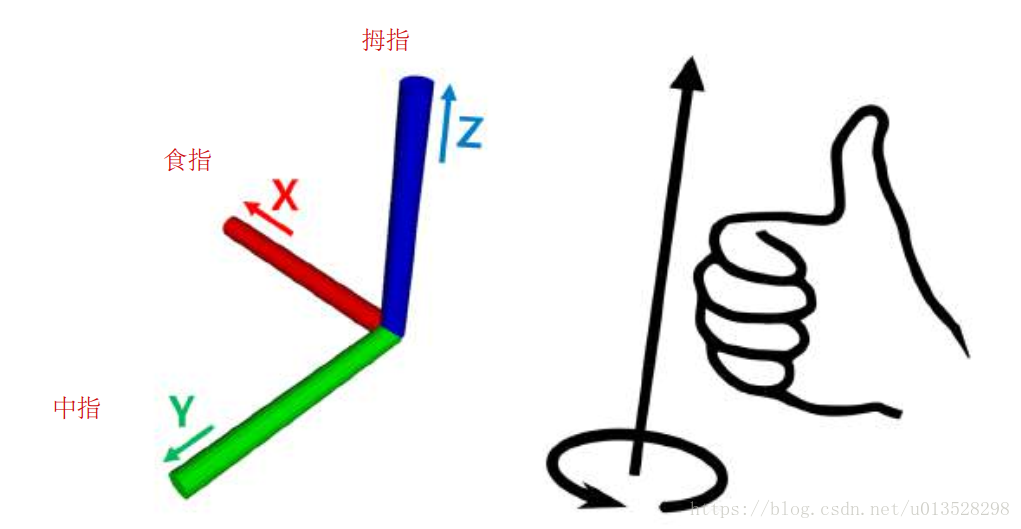
机器人中的旋转轴使用x,y和z轴。正面是x轴的正方向,轴是红色(Red)。左边是y轴的正方向,轴用绿色(Green)表示。最后,上方是z轴的正方向,轴用蓝色(Blue)表示。为了便于记忆,您可以将x轴视为食指,将y轴视为中指,将z轴视为拇指。顺序是x、y、z,且颜色是RGB颜色顺序。机器人的旋转方向是右手定则,用右手卷住的方向是正(+)方向
对于一个点,我们可以用(x,y,z)三个坐标值来描述,但是对于一个三维空间的刚体来说,假设有一个坐标系固结在刚体上,则需要三个向量去描述其姿态,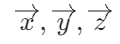 ,那么一整个刚体则需要四个向量去描述(3方向+1原点)
,那么一整个刚体则需要四个向量去描述(3方向+1原点)刚体可以由其在空间中相对参考坐标系的位置和方向(即位姿)进行完整的描述。
描述刚体的位姿最常用的方法是在基座上建立一个固定坐标系{A},在运动刚体上建立运动坐标系{B},通过描述运动坐标系在固定坐标系的位置和姿态来描述刚体的空间位姿。
刚体的空间位置可用运动坐标系的原点坐标
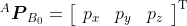
表示,运动坐标系的原点可以建立在刚体的质心或几何中心上,通过描述该点的坐标,可以很好地体现刚体的位置特征。
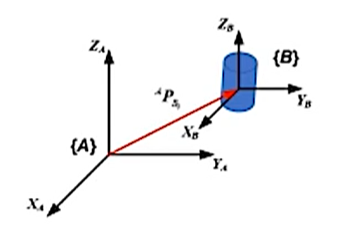
知道原点就可以知道刚体的位置,知道固结在刚体坐标系的指向,就可以知道刚体的姿态
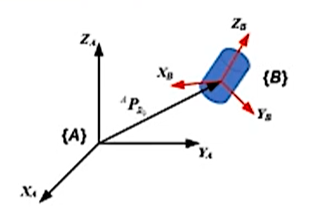

用于坐标系间点的映射的通用数学表达式称为算子,包括点的平移算子,矢量旋转算子,旋转加平移算子。
二、平移坐标系的映射:
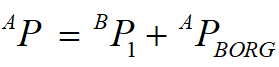 [图片]
[图片]
P1是在坐标系一开始的位置,P2是在经过平移算子的位置,
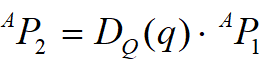
平移算子:
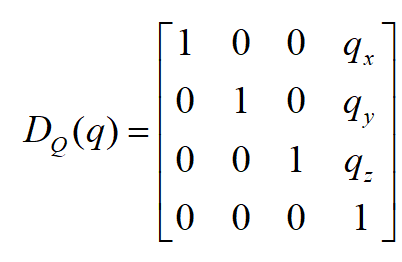
三、旋转
坐标系的映射:
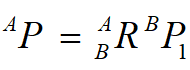
矢量变化直接就是将坐标系换成矢量即可,变换矩阵是相同的
这里只介绍欧拉角,因为这个欧拉角是指绕特定的X,Y,Z(笛卡尔坐标系),如果是然任意轴,其实旋量理论更方便,后面有机会再补充
那么旋转的欧拉角按从世界坐标系转换到本体坐标系的过程,先按z轴旋转、之后y轴旋转、之后x轴旋转,最终得到本体坐标系,得到的角度分别是yaw、pitch、roll,那么从本体坐标系到世界坐标系的旋转矩阵按如下方式定义:
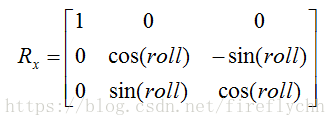

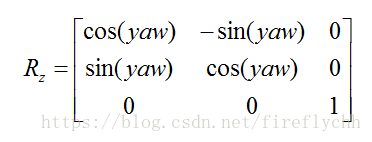
如果绕的这个轴一直是本体坐标系的轴,那么按顺序右乘,如果是按照相对坐标系,那就左乘,这个从定义去考虑就很简单,因为右乘就是指将前面的矩阵的列向量进行线性组合,列向量则是本体坐标系的基向量,而左乘则是,将后面的行向量进行线性组合。四、一般变换
坐标系的映射:
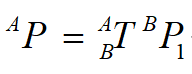
那这个T自然而然就是包括了旋转和平移,左上角A,右下角B 表示B相对于A来描述,
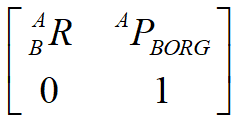
为什么要写成这个样子,因为这个矩阵能够旋转拉伸平移,集中在一起,参考图形的知识:

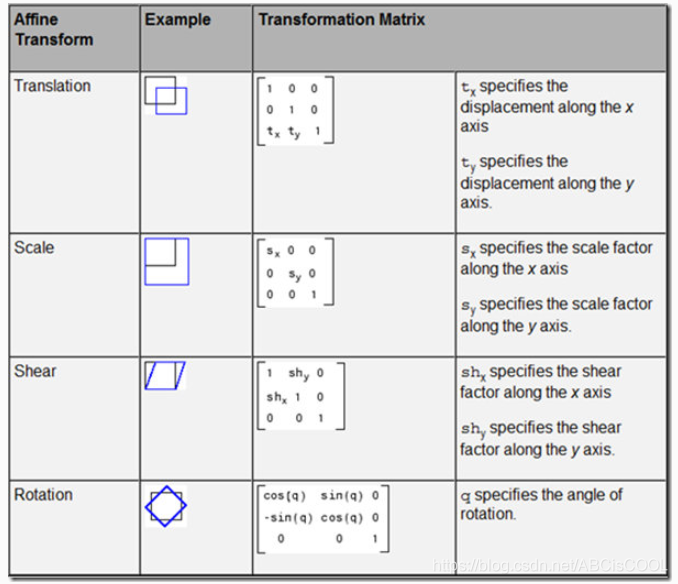
- 平移translation
- 缩放scaling
- 旋转rotation-
- 剪切shearing
- 投影变换projective transformations
- 自定义的变换custom transformations
只不过机器人学中把这个平移放在右上角而已,那为什么要把这个写成矩阵的形式呢?
首先对于对于矩阵 A 可以对角化的话,可以通过相似矩阵进行下面这样的特征值分解:
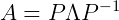
其中,P 的列向量是单位化的特征向量。
说的有点抽象,我们拿个具体的例子来讲:
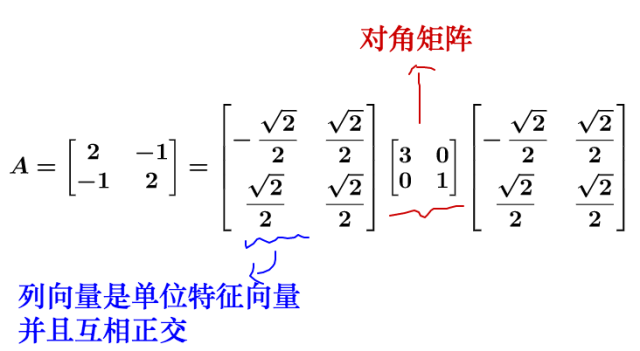
对于方阵而言,矩阵不会进行纬度的升降,所以矩阵代表的运动实际上只有两种:- 旋转
- 拉伸
最后的运动结果就是这两种的合成。
我们再回头看下刚才的特征值分解,实际上把运动给分解开了:
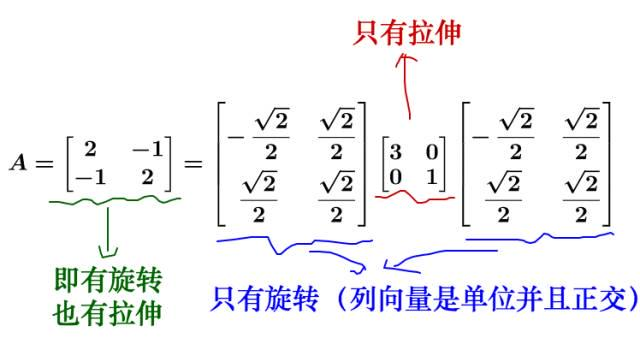
我们来看看在几何上的表现是什么,因此相似矩阵的讲解涉及到基的变换,所以大家注意观察基:
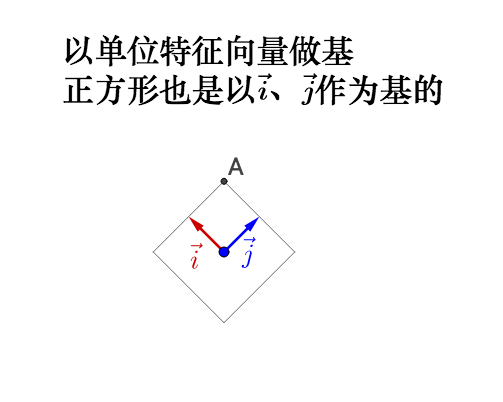
左乘
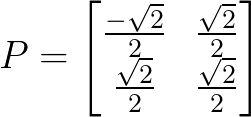
:
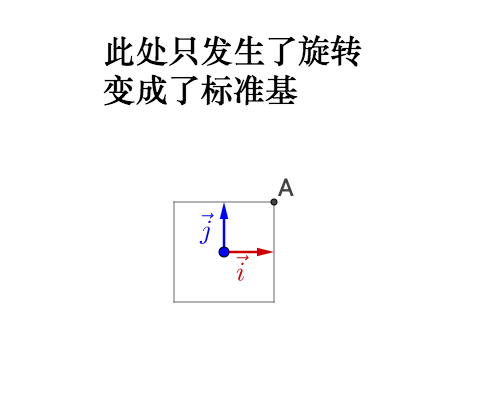
如果旋转前的基不正交,旋转之后变为了标准基,那么实际会产生伸缩,所以之前说的正交很重要。
继续左乘对角矩阵
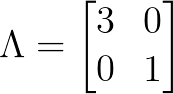
:
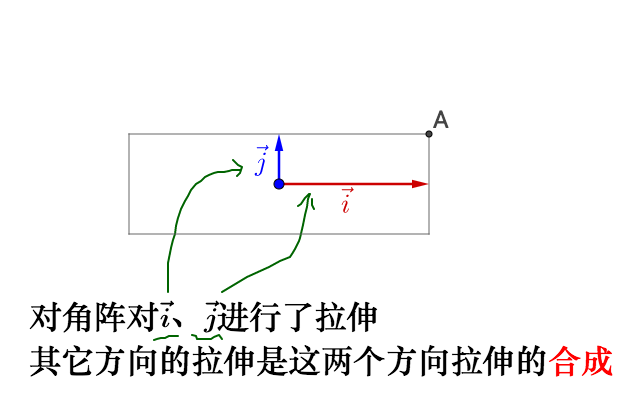
相当于,之前的旋转指明了拉伸的方向,所以我们理解了: - 特征值就是拉伸的大小
- 特征向量指明了拉伸的方向
回到我们之前说的运动上去,特征值就是运动的速度,特征向量就是运动的方向,而其余方向的运动就由特征向量方向的运动合成。所以最大的特征值对应的特征向量指明了运动速度的最大方向。
左乘
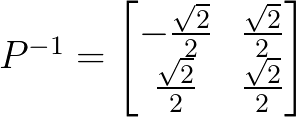
:
补充完对角阵的知识,我们就可以知道旋转矩阵就是这么一个旋转变换,而大部分的图形变换的矩阵是混合了拉伸,机器人学相比起来就是很简单的啦~~~
这里整体只需掌握几件事
- 刚体的描述
- 坐标系的变换映射
- 矢量的变换算子
- 写成矩阵的好处